Теорія многочленів

1)Вираз виду: ,
де - _______________________________________________,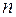

– _____________________________________,

- ___________________________________________,

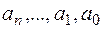називається ____________________ над ______________.

2) Степінь многочлена позначається ________ і канонічна форма многочлена це _________________________________________
_____________________________________________________.

3) Алгебраїчна рівність многочленів ________________________

_____________________________________________________,

а функціональна - ______________________________________

_____________________________________________________.

4) Якщо многочлени рівні алгебраїчно, то вони рівні і _________.

Чи справедливе обернене твердження: ___________________.

5) Властивості подільності многочленів:_____________________

______________________________________________________

______________________________________________________
______________________________________________________
_____________________________________________________.

6) Сформулювати теорему :_____________
______________________________________________________
_____________________________________________________.

7) Якщо , то а) - ____________________________,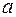

б) - ____________________________.

8) - _______________________________________________.

9) _______________________________________________.

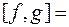10) Якщо , то _________________________________.

11) Заповнити пусті місця: ______+ _____,

де ___________________________________________________.

12) Многочлен з називається незвідним у полі , якщо ____________________________________________
_____________________________________________________.

13) Властивості незвідних многочленів: __________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________.

14) Якщо і 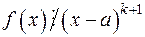, то _______________
_____________________________________________________.

15) Теорема Кронекера: _______________________________
___________________________________________________________________________________________________________.

16) Поле розкладу многочлена - це ______________________
___________________________________________________________________________________________________________.

17) Для того, щоб був коренем кратності 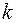многочлена необхідно і достатньо, щоб _________________________
______________________________________________________
_____________________________________________________.

18) Нехай

		-6		-6
		-3		-3

Що можна сказати про число ? Чому рівна остача від ділення многочлена на _______________________________________________.

19) Раціональний дріб називається правильним, якщо
_____________________________________________________.

Навести приклади правильного дробу: ____________________.

20) Елементарний дріб – це ____________________________
_____________________________________________________.

21) Якщо , то ______________,
де___________________________________________________.

22) Кожен правильний дріб виду , де - _______
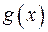_________________________, - ______________________ можна подати у вигляді _________________________________
_____________________________________________________.

23) Многочлен є многочленом від __________змінних. Його вищий член __________, степінь ___________, лексикографічний запис ___
_____________________________________________________.

24) Многочлен називається однорідним, якщо _____________
_____________________________________________________.

Приклад:_____________________________________________.

25) Многочлен є симетричним, якщо __________
_____________________________________________________.
Приклади симетричних многочленів: _____________________
_____________________________________________________.

Приклади несиметричних многочленів: ___________________
_____________________________________________________.

26) Властивості симетричних многочленів:__________________________________________
______________________________________________________
_____________________________________________________
_____________________________________________________.

27) Елементарні симетричні многочлени – це
а) для 2 змінних________________________________________
_____________________________________________________,
б) для 3 змінних________________________________________
_____________________________________________________.

28) Основна теорема симетричних многочленів:___________
______________________________________________________
_____________________________________________________.

29) Степеневу суму третього порядку від двох змінних представити через основні симетричні многочлени: _________
_____________________________________________________.

30) Теорема Вієта:_____________________________________
______________________________________________________
_____________________________________________________.

31) 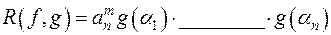, де - ______
______________________________________________________ Заповнити пропущені місця. Про що йде мова:______________
_____________________________________________________.

32) Якщо , то ________________________________
_____________________________________________________.

33) . Заповнити пропущені місця.

34) Якщо 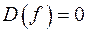, то _________________________________
_____________________________________________________.

35) Многочлен третього степеня над полем має:

а) принаймні один дійсний корінь;

б) два дійсних і один комплексний корені.

Підкреслити правильну відповідь. Чи існують інші варіанти? Якщо так, то вказати їх: _________________________________
_____________________________________________________.

36) Будь-який многочлен ненульового степеня з комплексними коефіцієнтами має_________________________
_____________________________________________________.

37) Многочлен 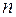-го степеня у полі С має _________________
_____________________________________________________.

38) Якщо 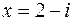є коренем , то і 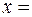_____________________.Сформулювати теорему на основі якої було зроблено висновок_____________________________
_____________________________________________________.

39) Що можна сказати про звідність довільного многочлена над , степінь якого перевищує 2: _______________________
_____________________________________________________.
А якщо степінь дорівнює 2:______________________________
_____________________________________________________.

40) Всі дійсні корені многочлена містяться в інтервалі: ______ ________, де __________________________________________.

41) Правило Декарта: _________________________________
______________________________________________________
_____________________________________________________.

42) Що означає відокремити дійсні корені многочлена: _____
_____________________________________________________.

43) Як утворюється ряд Штурма: _______________________
_____________________________________________________
_____________________________________________________.

44) Властивості ряду Штурма: _________________________
______________________________________________________
______________________________________________________
______________________________________________________
_____________________________________________________.

45) Теорема Штурма: __________________________________
______________________________________________________
_____________________________________________________.

46) Щоб число , де 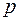- це___________________________,
- це_________________________________________було коренем рівняння з цілими коефіцієнтами, необхідно _______
_____________________________________________________.
Чи є ця умова достатньою? _____________________________.

47) Для того, щоб з цілими коефіцієнтами був звідним у полі необхідно і достатньо, щоб _______________________
_____________________________________________________.

48) Критерій Ейзенштейна: ____________________________
______________________________________________________
_____________________________________________________.

49) Число є алгебраїчним, якщо _____________________
____________________________, а трансцендентним - ______
_____________________________________________________.

50) Мінімальний многочлен – це многочлен, що задовольняє умови:___________________________________________________________________________________________________________________________________________________________.

Дата добавления: 2015-08-21