
Читайте также:
|
После ввода данных вызвать диалоговое окно П араметры … (рис 7.12)

Рис 7.12
Параметры, используемые по умолчанию, подходят для решения большинства задач. В нашем случае необходимо только установить флажок Л инейная модель, что обеспечивает применение симплекс-метода. ОК.
На экране вновь появится диалоговое окно Поиск решения. В ыполнить.
На экране появится диалоговое окно Результаты поиска решения. Решение найдено и результат оптимального решения задачи приведены в таблице (Рис. 7.14).

Рис 7.13
| A | B | C | D | E | F | G | H | |
| Переменные | ||||||||
| Имя | Прод1 | Прод2 | Прод3 | Прод4 | ||||
| Значение | ||||||||
| Нижн. гр. | ||||||||
| Верх. гр. | ЦФ | Направление | ||||||
| Коэф. в ЦФ | ||||||||
| Вид ресурсов | Ограничения | Лев. часть | Знак | Прав. часть | ||||
| Трудовые | <= | |||||||
| Сырье | <= | |||||||
| Финансы | <= |
Рис 7.14
Из рис. 7.14 видно, что в оптимальном решении Прод1=10, Прод2=0, Прод3=6, Прод4=0. При этом максимальная прибыль будет составлять 1320, а количество использованных ресурсов: трудовых=16, сырья=84, финансов=100.
7) Важным фактором, помогающим принять решение является графическое представление полученного результата.

Рис 7.15
8) Преодоление несовместности и анализ оптимального решения оставляем на самостоятельное изучение. Этот материал можно найти в [5].
Пример 2
Компания производит два основных типа товара (Изделие-1, Изделие-2). Изделие-1 требует 2 единицы сырья А и 2 ед. сырья В, оно приносит прибыль компании 2 д енежные е диницы. Изделие-2 требует 3 ед. сырья А и 5 ед. сырья В, оно приносит прибыль 4 д. е. Найдите оптимальный план производства, если доступно всего 1200 единиц сырья А и 1600 единиц сырья В.
Решение:
Пусть Х – количество производимого товара первого изделия, Y – количество производимого товара второго изделия. Составим математическую модель.

Создадим форму для ввода условий задачи и введем исходные данные:
| A | B | C | D | E | F | |
| Переменные | ||||||
| Имя | Изделие-1 | Изделие-2 | ||||
| Значения | ||||||
| Нижн. Гр. | ||||||
| Верх. Гр. | ЦФ | |||||
| Коэф. ЦФ | ||||||
| Ограничения | ||||||
| Вид | Левая часть | Знак | Правая часть | |||
| Сырье А | <= | |||||
| Сырье Б | <= |
Введем зависимости из математической модели:
| A | B | C | D | E | F | |
| Переменные | ||||||
| Имя | Изделие-1 | Изделие-2 | ||||
| Значения | ||||||
| Нижн. Гр. | ||||||
| Верх. Гр. | ЦФ | |||||
| Коэф. ЦФ | =СУММПРОИЗВ(B$3:C$3;B6:C6) | |||||
| Ограничения | ||||||
| Вид | Левая часть | Знак | Правая часть | |||
| Сырье А | =СУММПРОИЗВ(B$3:C$3;B9:C9) | <= | ||||
| Сырье Б | =СУММПРОИЗВ(B$3:C$3;B10:C10) | <= |
Назначение целевой функции, ввод ограничений и граничных условий.Вызвать диалоговое окно Поиск Решения: Сервис-Поиск решения…

Рис 7.16
Назначить целевую функцию: $D$6. Ввести адреса искомых переменных: $B$3:$C$3. Ввести ограничения и граничные условия: $D$9:$D$10<=$F$9:$F$10, $B$3:$C$3>=$B$4:$C$4. Вызвать диалоговое окно П араметры, установить флажок Л инейная модель. OK. Выполнить.
На экране появится диалоговое окно Результаты поиска решения (рис 7.13). OK. Результат оптимального решения задачи приведен в таблице
| A | B | C | D | E | F | |
| Переменные | ||||||
| Имя | Изделие-1 | Изделие-2 | ||||
| Значения | ||||||
| Нижн. Гр. | ||||||
| Верх. Гр. | ЦФ | |||||
| Коэф. ЦФ | ||||||
| Ограничения | ||||||
| Вид | Левая часть | Знак | Правая часть | |||
| Сырье А | <= | |||||
| Сырье Б | <= |
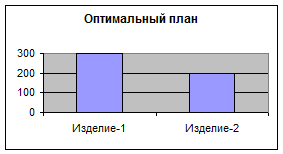
По полученным результатам построим гистограмму:
Дата добавления: 2015-10-31; просмотров: 118 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные положения симплекс-метода | | | Практическая работа 1 |