Практическая работа 1

Для данной задачи (см. Приложение 4) составить форму ввода (или загрузить из файла, подготовленного преподавателем), ввести исходные данные и зависимости из математической модели. Вызвать диалоговое окно Поиск решения, ввести адрес целевой функции, указать изменяемые ячейки, ввести ограничения и граничные условия. В диалоговом окне Параметры установить флажок Линейная модель. Запустить алгоритм поиска оптимального решения. По полученным результатам построить столбчатую гистограмму. Сформулировать вывод.

Транспортная задача

Введение

У некого предпринимателя, занимающегося производством и продажей холодильников, есть две фабрики, которые снабжают три его магазина. В начале месяца он получает от директора каждого из магазинов заявку на определенное число холодильников, в которых данный магазин нуждается в текущем месяце. Совокупность всех таких заявок позволяет установить общее число новых холодильников, которые нужно изготовить на этих двух фабриках. Для простоты мы предположим, что у предпринимателя достаточно ресурсов (рабочей силы, сырья и т. д.), чтобы выполнить все заявки, и что в данный момент отсутствует задел для продажи. Пусть первому магазину, обозначим его S₁, требуется 10 холодильников, магазину S₂ – 8 и магазину S₃ – 7, всего, таким образом, 25 холодильников. Пусть предприниматель решил изготовить 11 холодильников на первой фабрике F₁ и оставшиеся 14 на фабрике F₂. Задача состоит в том, чтобы выяснить, сколько холодильников нужно отправить с каждой фабрики в каждый магазин, чтобы общая стоимость всех перевозок была минимальной.

Основная форма этой задачи, известной под названием транспортной задачи, представляет собой одну из самых ранних и наиболее широко используемых формулировок линейного программирования.

Решение

Нам нужна дополнительная информация относительно транспортных ограничений и цен. Предположим, что можно отправить любое число холодильников с каждой фабрики в любой магазин, то есть что имеются транспортные пути (железные дороги, шоссе и т. п.), связывающие каждую фабрику со всеми магазинами. Предположим далее, что нам известна также стоимость перевозки одного холодильника с фабрики в магазин в каждом случае. Здесь мы должны принять допущение относительно линейности, которое в некоторых случаях весьма спорно и может вызвать критику. Предположение о линейности, или пропорциональности, состоит в том, что если стоимость перевозки одного холодильника из F₁ в S₁ составляет 10 долларов, то стоимость перевозки двух холодильников составляет 20 долларов, трех – 30 долларов и т. д. Против подобного допущения можно было бы возразить, основываясь на реальном опыте. Если нанять грузовик для перевозки одного холодильника стоит 100 долларов, то в случае двух холодильников стоимость перевозки каждого составит 50 долларов (не считая стоимости погрузочно-разгрузочных работ), в случае трех – 33 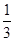доллара, то есть стоимость меняется нелинейно.

В большинстве транспортных ситуаций стоимость нелинейна, но с помощью того или иного усреднения можно получить хорошее линейное приближение.

Итак, в нашей задаче мы предполагаем, что стоимость перевозки холодильника между любой фабрикой и любым магазином известна (см. табл. 1) и линейна. Транспортные задачи имеют, как и любая задача оптимизации, много допустимых решений.

Мы ищем решение, которое удовлетворяет принятым ограничениям (11 холодильников должны быть отправлены из F₁, 14 холодильников—из F₂, S₁ получает 10, S₂ – 8 и S₃ – 7 холодильников) и одновременно минимизирует меру эффективности – общую стоимость всех перевозок.

Чтобы дать математическую постановку задачи, мы сведем всю информацию в две таблицы:

		S1	S2	S3					S1	S2	S3
F1		$8	$6	$10			F1		?	?	?
F2		$9	$5	$7			F2		?	?	?
Таблица 1			Таблица 2

В таблице 1 заданы стоимости перевозок, а в таблице 2 клетки со знаком? соответствуют неизвестному числу холодильников, которые нужно перевезти с данной фабрики в определенный магазин. В дальнейшем в подобных таблицах будем опускать первую строку и первый столбец.

Приведем два допустимых решения этой задачи:

Решение 1			Решение 2

Можно попытаться найти и другие решения самостоятельно.

Числа, стоящие в белых ячейках первой таблицы, соответствуют решению задачи, при котором из F₁ в магазины отправлено 10+1+0=11 холодильников, а из F₂, 0+7+7==14 холодильников. Общее число холодильников, полученных магазином S₁ с обеих фабрик, равно 10+0=10, магазином S₂ 1+7=8 и S₃ 0+7 = 7 холодильников. Второй вариант решения аналогичен. В предположении, что стоимость перевозок линейна, мы получим, что общая стоимость в первом случае равна 8·10+6·1+5·7+7·7=170 (долларов), а во втором случае 6·7+10·4+9·10+5·1+7·3=198 (долларов).

Таким образом, в первом случае затраты на перевозку холодильников меньше, чем во втором, однако не ясно, нет ли другого допустимого решения, позволяющего еще больше снизить затраты на перевозку. Методы линейного программирования позволяют утверждать, что минимум существует и его можно найти. В нашей задаче минимум затрат на перевозку холодильников достигается в первом решении.

Для построения математической модели транспортной задачи необходимо ввести некоторые математические сокращения. Пусть x₁₁ означает число (пока еще не известное) холодильников, отправленных из F₁ в S₁, x₁₂ — число холодильников, отправленных из F₁ в S₂, и т. д. В общем случае х_ij – это число холодильников, отправленных с фабрики F_i в магазин S_j,. Введем эти обозначения в нашу таблицу:

	x11	x12	x13
	x21	x22	x23

Теперь очень просто построить математическую модель. Из F₁ отправлено x₁₁, x₁₂ и x₁₃ холодильников, всего 11 штук. Аналогично из F₂ отправлено x₂₁, x₂₂ и x₂₃ холодильников, всего 14 штук. Поскольку требуется всего 25 холодильников (10+8+7) и произведено их ровно 25 (11+14), то все холодильники с каждой фабрики должны быть отправлены в магазины. Таким образом, общее число холодильников, отправленных из F₁, дается уравнением x₁₁+x₁₂+x₁₃=11, а из F2 – x₂₁+x₂₂+x₂₃=14. Эти суммы получаются путем сложения по строкам чисел, стоящих в таблице.

Поскольку каждый магазин получает столько холодильников, сколько заказывает, то общее количество холодильников, полученное каждым магазином (оно находится суммированием по столбцам), задается уравнениями

x₁₁+x₂₁=10 для S1,

x₁₂+x₂₂=8 для S2,

x₁₃+x₂₃=7 для S3.

Для каждого набора чисел x_ij где i снова означает номер фабрики, а j – номер магазина, общая стоимость перевозок равна

8x₁₁+6x₁₂+10x₁₃+9x₂₁+5x₂₂+7x₂₃ (долларов).

Эти уравнения представляют собой основные ограничения нашей математической модели. Единственное наше упущение состоит в том, что мы не ограничили x_ij так, чтобы они могли принимать только положительные и нулевые значения. Отрицательные x_ij, означали бы, что холодильники перевозятся из магазина на фабрику, то есть общее число холодильников больше того, которое произведено на фабриках. Мы исключаем такую возможность, вводя ограничения x_ij³0 (x_ij больше или равно нулю). Поскольку мы хотим определить множество значений x_ij³0, удовлетворяющих уравнениям и минимизирующих общую стоимость, то имеем следующую математическую модель – модель линейного программирования данной транспортной задачи:

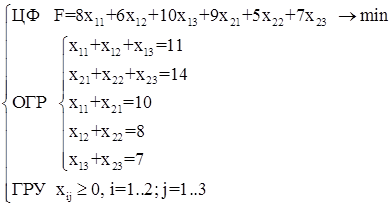
Каждая фабрика и магазин порождают уравнение, связывающее между собой те переменные, которые относятся к данной фабрике или магазину. Эти уравнения, так же как и целевая функция, линейны, поскольку они представляют собой просто суммы переменных. Общее количество переменных равно произведению числа фабрик на число магазинов, в нашем случае 2·3=6. Аналогично число уравнений равно сумме числа фабрик и магазинов; в нашем случае оно равно 5. Транспортные задачи могут быть очень громоздкими, и здесь на помощь придет ЭВМ.

До сих пор молчаливо предполагалось, что x_ij должны быть целыми (мы не в состоянии перевезти 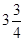холодильника!). Можно строго показать, что если количество фабрик и магазинов выражается целыми числами, то и сама транспортная задача будет допускать оптимальное решение в целых числах. Разумеется, утверждать, что так будет всегда, в любой задаче линейного программирования, нельзя. Возможность решения транспортной задачи в целых числах обусловлена особой структурой уравнений соответствующей ей математической модели.

Нашу модель мы описывали на конкретном примере и поэтому вынуждены были говорить о фабриках, магазинах и холодильниках, однако эти детали не имеют значения. Все рассуждения остаются в силе и в более общем случае, если рассматривать пункты отправления (фабрики), пункты назначения (магазины) и однородные единицы, подлежащие перевозке (холодильники), а также некую меру, которую необходимо минимизировать (общая стоимость перевозок).

Пример

Заданы стоимости перевозок в у.е. одного комплекта товара (мебель) в таблице 1. Доставки осуществляет фирма "Айсберг" от 4 поставщиков товаров, которые расположены соответственно: в Архангельске, Кандалакше и Петрозаводске на 5 оптовых баз разных фирм, которые находятся в Мурманской области. Кроме того задано количество комплектов товаров (наличие – 15), которое может купить каждая фирма от поставщика. И потребность каждой оптовой базы в определенном количестве комплектов товара (потребность – 12), для обеспечения нормальной работы. За одну поездку можно перевезти один комплект товара. Определить оптимальный план работы фирмы "Айсберг".

		Оптовая база 1	Оптовая база 2	Оптовая база 3	Оптовая база 4	Оптовая база 5
Архангельск
Кандалакша
Петрозаводск
Петрозаводск

Решение:

Дата добавления: 2015-10-31