Методы решения задач.

Задача линейного программирования, которая является частным случаем задачи оптимизации записывается следующим образом:

(7.10)

Дана система из n линейных неравенств с n неизвестными и линейная функция F. Требуется найти решение системы x₁, x₂, x₃…x_n, удовлетворяющей ГРУ, при котором функция F принимает max значение.

Задачи линейного программирования можно решить аналитическим путем и графическим методом. Второй метод – наглядный, но пригоден лишь для n=2 (т.е. где число переменных = 2).

Пример.

Известно, что уравнение прямой имеет вид: a₁x₁+a₂x₂=b. Построим прямую 2x₁+x₂=2. Перепишем это уравнение в виде: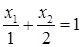

При такой форме записи в знаменателе показаны отрезки, которые отсекает прямая на осях координат (Рис. 7.2). Если от исходного уравнения перейти к неравенству 2x₁+x₂£2, то графически решение этого неравенства показано на рис. 7.3, т.е. решением линейного неравенства с двумя переменными является полуплоскость. На рис. 7.3 часть плоскости, которая не удовлетворяет неравенству расположена выше прямой, заштрихована. Координаты всех точек, принадлежащих не заштрихованной части плоскости, имеют такие значения х₁ и х₂, которые удовлетворяют заданному неравенству. Эта полуплоскость является областью допустимых решений (ОДР).

Рассмотрим систему неравенств:

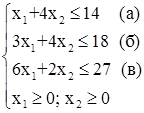
Для удобства запишем ее в следующем виде:

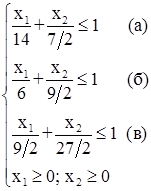
Графическое решение этой системы показано на рис. 7.4

Решением этой системы являются координаты всех точек, принадлежащих ОДР, т.е. многоугольнику ABCDO.

Т.к. в ОДР бесчисленное множество точек, значит, рассматриваемая система имеет бесчисленное множество допустимых решений.

Если мы хотим найти оптимальное решение, то мы должны принять целевую функцию. Пусть мы хотим, чтобы решение было оптимальным в смысле максимизации целевой функции F=x₁+x₂ → max

Эта зависимость на рис. 7.5 представлена в форме уравнения прямой с угловым коэффициентом x₂=F–x₁, из которого видно, что tga= –1. При этом угол a=135°, а величина F равна отрезку, отсекаемому прямой на оси ординат. Если прямую перемещать параллельно самой себе в направлении, указанном стрелками, то величина F будет возрастать. Совместим теперь ОДР, изображенную на рис. 7.4, с линией целевой функции F, построенной на рис. 7.5, получим рис. 7.6.

Поскольку требуется найти оптимальное решение, при котором целевая функция F=x₁+x₂®max, т.е. стремится к максимуму, будем перемещать график целевой функции в направлении увеличения F. Очевидно, что оптимальным решением будут координаты точки С, равные х₁^* и х₂^*. При этом F=F^*.

На основании рассмотренного можно сделать вывод:
оптимальным решением являются координаты вершин ОДР.

На этом базируется аналитический метод решения задач линейного программирования, который заключается в следующем:

r Найти вершины ОРД, как точки пересечения ограничений.

r Определить последовательно значения целевой функции в вершинах.

r Вершина, в которой ЦФ приобретает оптимальное (максимальное или минимальное) значение, является оптимальной вершиной.

r Координаты этой вершины и являются искомыми оптимальными значениями переменных.

Дата добавления: 2015-10-31