Пространство функций, суммируемых со степенью p.

Пусть - ограниченное, измеримое множество и - измеримая функция.

Определение 4.3.1. Функция называется суммируемой со степенью , если .

Определение 4.3.2. Числа называются сопряженными показателями, есл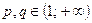и и .

Символом 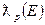обозначим множество всех функций суммируемых со степенью . Приведем без доказательства неравенства Гельдера и Минковского.

Терема 4.3.1. (Неравенство Гельдера).

Пусть - сопряженные показатели и , , тогда произведение функций является суммируемой функцией, при этом справедливо неравенство

. (4.3.1)

Отметим, что неравенство Гельдера является обобщением неравенства Коши-Буняковского. Действительно, при значениях сопряженных показателей 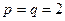неравенство Гельдера совпадает с неравенством Коши-Буняковского.

Теорема 4.3.2. (неравенство Минковского).

Если и , то сумма функций 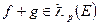, причем справедливо неравенство

(4.3.2)

Очевидно, что вместе с любой функцией множество 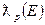содержит все функции вида , где - произвольный скалярный множитель. Теорема 4.3.2 утверждает, что сумма любых двух функций суммируемых со степенью по Лебегу является также элементом множества .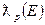

Таким образом, множество 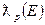замкнуто относительно операций умножения на скалярный множитель и сложения элементов.

Вместо множества 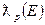будем рассматривать множество классов эквивалентных функций , которое является линейным пространством. Пространство становится нормированным, если норму элемента определить равенством

.

На вопрос: Как соотносятся пространства и , если дает ответ следующая

Теорема 3.3.3. Пусть . Тогда .

Доказательство. Произвольно выберем элемент 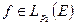и покажем, что . С этой целью используем неравенство Гельдера

,

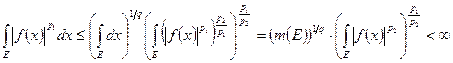здесь - показатель сопряженный показателю 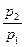, т.е. .

Теорема доказана.

Таким образом, Лебеговы пространства определены для любого показателя , при этом чем больше показатель, тем более «узким» становится пространство, т.е.

.

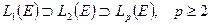Дата добавления: 2015-10-30