
Читайте также:
|
В этом пункте мы определим понятие интеграла Лебега.
Напомним, что интегралом Римана от функции  называется предел интегральной суммы
называется предел интегральной суммы
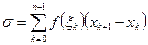 , при
, при  ,
,
при условии, что этот предел не зависит от способа разбиения отрезка на части и выбора промежуточных точек  .
.
Для интегрируемости функции необходимо, чтобы она обладала тем свойством, что смена промежуточной точки не сильно бы меняла значение самой интегральной суммы. Поэтому вполне естественным выглядит тот факт, что непрерывная функция является интегрируемой по Риману.
Простым примером функции не интегрируемой по Риману является функция Дирихле
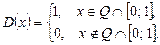
Если в качестве промежуточных точек будут выбраны рациональные числа, то значение интегральной суммы равно единице, при выборе промежуточных точек иррациональными, интегральная сумма становится равной нулю. Таким образом, предел интегральных сумм для функции Дирихле зависит от выбора промежуточных точек  , следовательно, функция Дирихле не интегрируема по Риману.
, следовательно, функция Дирихле не интегрируема по Риману.
Перейдем к построению интегральных сумм Лебега.
Пусть  - измеримая ограниченная функция. Тогда найдутся такие числа
- измеримая ограниченная функция. Тогда найдутся такие числа 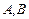 , что для любого
, что для любого  , справедливы неравенства
, справедливы неравенства 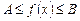
Разделим отрезок  точками
точками 

на 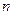 промежутков и рассмотрим множества
промежутков и рассмотрим множества 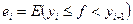 ,
, 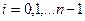 .
.
Множества 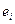 обладают свойствами:
обладают свойствами:
1)  , если
, если 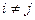 ;
;
2) 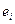 измеримы как пересечение двух измеримых множеств;
измеримы как пересечение двух измеримых множеств;
3) 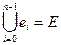 ;
;
4) 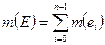 .
.
Данному разбиению поставим в соответствие число  .
.
Определим верхнюю и нижнюю интегральные суммы Лебега соответственно равенствами
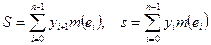 .
.
Приведем некоторые свойства интегральных сумм Лебега.
Лемма 3.1.1. Если к данному разбиению отрезка  добавить новые точки разбиения, то нижняя сумма не уменьшится, а верхняя не увеличится.
добавить новые точки разбиения, то нижняя сумма не уменьшится, а верхняя не увеличится.
Доказательство. Проведем для частного случая добавления одной точки на  -ом интервале. Тогда все слагаемые двух интегральных суммы
-ом интервале. Тогда все слагаемые двух интегральных суммы 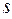 и
и  совпадают, а слагаемому
совпадают, а слагаемому 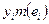 первой суммы отвечает два слагаемых второй суммы
первой суммы отвечает два слагаемых второй суммы  , причем
, причем 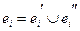 и
и  . Поэтому
. Поэтому  . Отсюда
. Отсюда 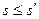 .
.
Аналогично доказывается утверждение для верхней интегральной суммы.
Лемма доказана.
Лемма 3.1.2. Любая нижняя интегральная сумма не превосходит любой верхней интегральной суммы Лебега.
Доказательство. Пусть двум различным разбиениям I и II соответствуют интегральные суммы  и
и 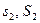 . Построим разбиение III, добавляя к точкам разбиения I точки второго разбиения. Согласно лемме 3.1.1 справедлива цепь неравенств
. Построим разбиение III, добавляя к точкам разбиения I точки второго разбиения. Согласно лемме 3.1.1 справедлива цепь неравенств
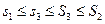 .
.
Таким образом,  .
.
Лемма доказана.
Далее рассмотрим последовательность разбиений, в которой к каждому предыдущему разбиению добавляются новые точки, таким образом, что 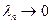 . Соответствующая последовательность нижних интегральных сумм Лебега
. Соответствующая последовательность нижних интегральных сумм Лебега 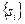 является не убывающей, ограниченной сверху любой верхней суммой Лебега. По теореме Вейерштрасса существует конечный предел нижних интегральных сумм Лебега
является не убывающей, ограниченной сверху любой верхней суммой Лебега. По теореме Вейерштрасса существует конечный предел нижних интегральных сумм Лебега
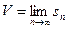 .
.
Аналогичными рассуждениями можно показать, что существует конечный предел верхних интегральных сумм
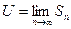 .
.
Покажем, что 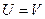 .
.
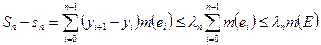 .
.
Так  , то
, то 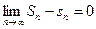 . Иными словами,
. Иными словами, 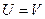 .
.
Определение 3.1.1. Общее значение пределов интегральных сумм Лебега называется интегралом Лебега от функции  на множестве
на множестве  . А функцию
. А функцию  называют интегрируемой по Лебегу на множестве
называют интегрируемой по Лебегу на множестве  .
.
Таким образом, доказана
Теорема 3.1.1. Любая измеримая ограниченная функция интегрируема по Лебегу.
В качестве примера рассмотрим процедуру нахождения интеграла Лебега от функции Дирихле. С этой целью построим разбиение отрезка 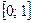

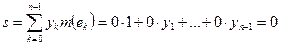 ,
,  .
.
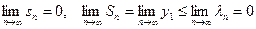 .
.
Таким образом, 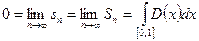 .
.
Дата добавления: 2015-10-30; просмотров: 206 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Измеримые функции. | | | Теорема 3.2.2. (аддитивность относительно области интегрирования). |