
Читайте также:
|
Введенная мера Лебега ограниченного множества обладает рядом свойств. Сформулируем и докажем некоторые из них.
Теорема 1.3.1. (Регулярность меры) Пусть 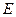 - ограниченное, измеримое множество. Для любого
- ограниченное, измеримое множество. Для любого  найдутся такие замкнутое множество
найдутся такие замкнутое множество 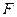 и открытое множество
и открытое множество 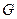 , что справедливы включения
, что справедливы включения  и неравенства
и неравенства
 .
.
Утверждение теоремы непосредственно следует из определения точных верхней и нижней граней числового множества.
Теорема 1.3.2. (Инвариантность меры) Если 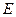 - измеримое множество и
- измеримое множество и  - произвольное число, то множество
- произвольное число, то множество  измеримо, причем
измеримо, причем  .
.
Доказательство. Согласно теореме 1.3.1, для произвольного  , найдутся такие открытое множество
, найдутся такие открытое множество 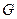 и замкнутое множество
и замкнутое множество 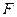 , что
, что  и
и
 .
.
Множества  и
и  являются замкнутым и открытым соответственно. При этом справедливы включения
являются замкнутым и открытым соответственно. При этом справедливы включения 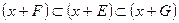 .
.
Покажем, что мера открытого множества 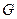 инвариантна относительно сдвига. Как открытое множество, множество
инвариантна относительно сдвига. Как открытое множество, множество 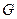 представимо в виде
представимо в виде  . Тогда
. Тогда  и
и  .
.
Замкнутое множество 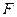 имеет представление
имеет представление 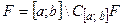 .
.
Отсюда  и
и  .
.
Как показано выше, мера открытого множества  инвариантна относительно сдвига, поэтому
инвариантна относительно сдвига, поэтому
 .
.
В конечном итоге получаем
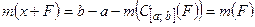 .
.
Таким образом, для любого  справедливо неравенство
справедливо неравенство
 .
.
Сопоставляя полученное неравенство с неравенством (1.3.1), и учитывая произвольность выбора  , делаем вывод, что
, делаем вывод, что  .
.
Теорема доказана.
Теорема 1.3.3. (монотонность меры) Если  - ограниченные измеримые множества и
- ограниченные измеримые множества и  , то
, то
 .
.
Теорема 1.3.4. (счетная аддитивность) Если ограниченное множество 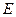 является объединением не более чем счетного числа ограниченных измеримых множеств
является объединением не более чем счетного числа ограниченных измеримых множеств  , и эти множества попарно не пересекаются, то множество
, и эти множества попарно не пересекаются, то множество 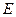 измеримо, причем
измеримо, причем
 .
.
Доказательство. Согласно теореме 1.2.1 для произвольного ограниченного множества 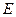 справедливо неравенство
справедливо неравенство 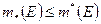 .
.
Покажем справедливость неравенства 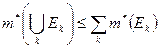 . С этой целью произвольно зафиксируем
. С этой целью произвольно зафиксируем  . В соответствии с утверждением теоремы 1.3.1 для каждого множества
. В соответствии с утверждением теоремы 1.3.1 для каждого множества  найдется такое открытое множество
найдется такое открытое множество  , что
, что
 и
и  .
.
Можно показать, что если множества  попарно не пересекаются, то
попарно не пересекаются, то 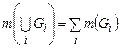 , в случае непустого попарного пересечения множеств
, в случае непустого попарного пересечения множеств  , справедливо неравенство
, справедливо неравенство  .
.
Так как  , то, по теореме 1.3.3, имеем
, то, по теореме 1.3.3, имеем
 .
.
В силу произвольности выбора  , можем заключить
, можем заключить  .
.
Аналогично можно показать, что  .
.
В итоге имеем цепь неравенств

из которой следует, что 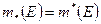 . Иными словами, множество
. Иными словами, множество  измеримо.
измеримо.
Теорема доказана.
Теорема 1.3.5. (Полуаддитивность меры) Для произвольных измеримых множеств  справедливо неравенство
справедливо неравенство
 .
.
Доказательство. Введем множества  ,
,  ,
,  .
.
Множество  представимо в виде
представимо в виде  . При этом множества
. При этом множества  попарно не пересекаются и измеримы как разность двух измеримых множеств (см. упражнение 10). Согласно теореме 1.3.4 множество
попарно не пересекаются и измеримы как разность двух измеримых множеств (см. упражнение 10). Согласно теореме 1.3.4 множество 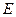 измеримо.
измеримо.
Докажем справедливость неравенства  . С этой целью произвольно зафиксируем
. С этой целью произвольно зафиксируем  . В соответствии с утверждением теоремы 1.3.1 для каждого множества
. В соответствии с утверждением теоремы 1.3.1 для каждого множества  найдется такое открытое множество
найдется такое открытое множество  , что
, что  и
и  .
.
Так как  , то в силу монотонности меры (Т. 1.3.3),
, то в силу монотонности меры (Т. 1.3.3),
 .
.
В силу произвольности выбора  имеем
имеем  .
.
Теорема доказана.
Теорема 1.3.6. Пусть множества  измеримы и
измеримы и  . Если множество
. Если множество  ограничено, то оно измеримо, причем
ограничено, то оно измеримо, причем  .
.
Доказательство. Множество  представим в виде
представим в виде
 .
.
Множества  и
и 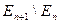 при
при 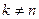 не пересекаются, поэтому, в силу теоремы 1.3.4, имеем
не пересекаются, поэтому, в силу теоремы 1.3.4, имеем
 .
.
Можно показать, что если 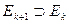 , то
, то
 .
.
С учетом последнего равенства  .
.
В силу ограниченности множества 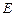 ряд
ряд  сходится и его частичная сумма равна
сходится и его частичная сумма равна  .
.
Поэтому 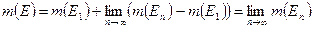 .
.
Теорема доказана.
Как следствие теоремы 1.3.6 получим следующее утверждение.
Теорема 1.3.7. Пусть  - измеримые множества и
- измеримые множества и  . Если при этом
. Если при этом  , то
, то  .
.
Доказательство. Множество  измеримо и потому ограничено, поэтому существует
измеримо и потому ограничено, поэтому существует  . Для дополнений множеств
. Для дополнений множеств 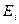 до отрезка
до отрезка  выполнены все условия предыдущей теоремы. Действительно,
выполнены все условия предыдущей теоремы. Действительно,  измеримы,
измеримы, 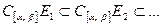 и
и  .
.
В силу теоремы 1.3.6 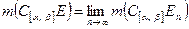 .
.
С другой стороны 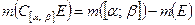 .
.
Отсюда  .
.
Теорема доказана.
Определение 1.3.1. Множество, представимое в виде пересечения или объединения не более чем счетного числа замкнутых множеств называется борелевским множеством типа 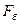 , а множество представимое в виде пересечения или объединения не более чем счетного числа открытых множеств называется борелевским множеством типа
, а множество представимое в виде пересечения или объединения не более чем счетного числа открытых множеств называется борелевским множеством типа  .
.
Справедлива
Теорема 1.3.8. (структура измеримого множества) Для любого ограниченного и измеримого множества 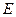 найдутся множества
найдутся множества 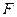 типа
типа 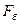 и
и 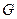 типа
типа  такие, что
такие, что
 и
и  ,
,  .
.
Теорема 1.3.8 утверждает, что всякое ограниченное измеримое множество является множеством типа 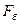 или
или  с точностью до множества нулевой меры.
с точностью до множества нулевой меры.
Доказательство. Согласно свойству регулярности меры, для произвольного натурального числа 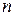 найдется такое открытое множество
найдется такое открытое множество  , что
, что  . Отсюда
. Отсюда 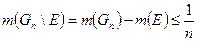 .
.
Множество  является борелевским множеством типа
является борелевским множеством типа 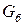 и
и  для любого
для любого  .
.
В силу монотонности меры,  при
при  .
.
Таким образом,  .
.
Аналогично можно доказать второе утверждение теоремы.
Теорема доказана.
Дата добавления: 2015-10-30; просмотров: 407 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Мера Лебега ограниченных множеств на числовой прямой. | | | Упражнения к главе 1. |