
Читайте также:
|
Пусть  - некоторое подмножество множества
- некоторое подмножество множества  .
.
Определение 1.1.1. Интервал  называется составляющим интервалом множества
называется составляющим интервалом множества  , если
, если
1)  ,
,
2) 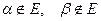 .
.
Например, множество 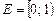 не имеет составляющих интервалов, а множество
не имеет составляющих интервалов, а множество  имеет один составляющий интервал
имеет один составляющий интервал 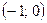 .
.
Справедлива
Лемма 1.1.1. Два составляющих интервала одного множества или не пересекаются, или совпадают.
Доказательство. Пусть множество  имеет два пересекающихся составляющих интервала
имеет два пересекающихся составляющих интервала 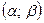 и
и  , т.е. существует такое число
, т.е. существует такое число 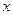 , что
, что  и
и  . Иными словами, концы интервалов удовлетворяют соотношению
. Иными словами, концы интервалов удовлетворяют соотношению  .
.
Если 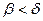 , то
, то 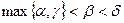 , поэтому
, поэтому  . Таким образом, интервал
. Таким образом, интервал 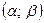 не является составляющим интервалом множества
не является составляющим интервалом множества  . Полученное противоречие приводит к выводу, что предположение
. Полученное противоречие приводит к выводу, что предположение 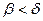 не верно.
не верно.
Если  , то
, то  . Отсюда следует, что
. Отсюда следует, что  не является составляющим интервалом множества
не является составляющим интервалом множества 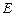 . Полученное противоречие отвергает предположение
. Полученное противоречие отвергает предположение  .
.
Таким образом, 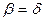 .
.
Проводя аналогичные рассуждения относительно левых концов составляющих интервалов, приходим к выводу 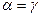 .
.
Доказано, что два составляющих интервала имеющие непустое пересечение совпадают.
Структура любого открытого ограниченного множества на числовой прямой описана в следующей теореме.
Теорема 1.1.1. Каждое непустое ограниченное открытое множество на прямой представимо в виде объединения не более чем счетного числа составляющих интервалов.
Доказательство. Пусть 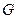 - ограниченное непустое открытое множество. И пусть
- ограниченное непустое открытое множество. И пусть 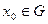 - произвольная точка множества. Покажем существование составляющего интервала, содержащего точку
- произвольная точка множества. Покажем существование составляющего интервала, содержащего точку  . В силу открытости и ограниченности множества
. В силу открытости и ограниченности множества 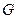 , множество
, множество  является непустым замкнутым множеством. Множество
является непустым замкнутым множеством. Множество 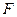 ограничено снизу числом
ограничено снизу числом  , т.е. для любого
, т.е. для любого  справедливо неравенство
справедливо неравенство 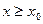 . Следовательно, существует
. Следовательно, существует  . Но так как
. Но так как  , то
, то  .
.
Предположим, что  , тогда существует такой
, тогда существует такой  , что
, что 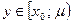 и
и  . Очевидно, что
. Очевидно, что 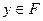 . Поэтому
. Поэтому 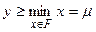 . Таким образом, элемент
. Таким образом, элемент  удовлетворяет двум противоречащим неравенствам. Следовательно, предположение
удовлетворяет двум противоречащим неравенствам. Следовательно, предположение  не верно.
не верно.
Аналогично можно показать существование такого  , что
, что 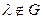 и
и 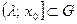 .
.
Таким образом, показано существование такого интервала  , что
, что  и
и 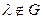 ,
, 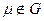 . По определению,
. По определению,  является составляющим интервалом множества
является составляющим интервалом множества 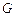 . Согласно лемме 1.1.1 каждая точка множества попадает только в один интервал.
. Согласно лемме 1.1.1 каждая точка множества попадает только в один интервал.
Для доказательства того факта, что любое ограниченное открытое множество представимо в виде объединения не более чем счетного числа составляющих интервалов, выберем в каждом составляющем интервале по одному рациональному числу. Тем самым установим взаимнооднозначное соответствие между числом составляющих интервалов и некоторым подмножеством множества рациональных чисел.
В силу того, что любое подмножество рациональных чисел не более чем счетно, можно сделать вывод, что число составляющих интервалов любого ограниченного открытого множества не более чем счетно.
Теорема доказана.
Отметим справедливость обратного утверждения:
Всякое множество являющееся объединением не более чем счетного числа взаимно не налегающих интервалов, является открытым.
Рассмотрим ограниченное замкнутое множество 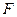 на числовой прямой.
на числовой прямой.
Числа 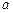 и
и  определим равенствами
определим равенствами

В силу ограниченности множества 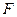 числа
числа 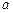 ,
,  конечны и
конечны и 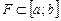 .
.
Дополнение  множества
множества 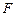 до отрезка
до отрезка 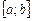 является открытым и имеет структуру, описанную в теореме 1.1.1. Поэтому справедлива
является открытым и имеет структуру, описанную в теореме 1.1.1. Поэтому справедлива
Теорема 1.1.2. Всякое непустое замкнутое ограниченное множество 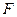 на прямой или является отрезком, или получается из некоторого отрезка удалением не более чем счетного числа не налегающих интервалов, концы которых принадлежат множеству
на прямой или является отрезком, или получается из некоторого отрезка удалением не более чем счетного числа не налегающих интервалов, концы которых принадлежат множеству 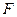 .
.
Отметим, что изолированные точки замкнутого множества появляются при удалении двух интервалов с общим концом.
Дата добавления: 2015-10-30; просмотров: 483 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вспомогательные определения и утверждения. | | | Мера Лебега ограниченных множеств на числовой прямой. |