
Читайте также:
|
Пусть  - измеримое, ограниченное множество.
- измеримое, ограниченное множество.
Определение 4.2.1. Измеримая функция  называется суммируемой с квадратом, если интеграл Лебега от квадрата функции конечен, т.е.
называется суммируемой с квадратом, если интеграл Лебега от квадрата функции конечен, т.е.
 .
.
Символом  обозначим множество всех функций суммируемых с квадратом.
обозначим множество всех функций суммируемых с квадратом.
Справедлива
Теорема 3.2.1. Всякая суммируемая с квадратом функция суммируема, т.е.  .
.
Доказательство. Из неравенств  и
и  следует, что
следует, что
 и
и  .
.
Поэтому  . Интегрируя полученное неравенство, получаем
. Интегрируя полученное неравенство, получаем
 .
.
Теорема доказана.
Справедлива
Теорема 4.2.2. Произведение двух суммируемых с квадратом функций есть суммируемая функция, т.е. если  , то
, то  .
.
Доказательство. Для произвольных  неравенство
неравенство  справедливо почти всюду. Интегрируя левую и правую часть неравенства, получаем
справедливо почти всюду. Интегрируя левую и правую часть неравенства, получаем
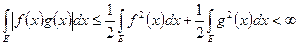 .
.
Теорема доказана.
Используя утверждение теоремы 4.2.2, покажем, что любая линейная комбинация функций суммируемых с квадратом является функцией принадлежащей тому же множеству  .
.
Теорема 4.2.3. Если  , то функции
, то функции  и
и 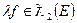 , где
, где  - произвольный скалярный множитель.
- произвольный скалярный множитель.
Доказательство. В силу свойства однородности операции интегрирования по Лебегу, вместе с любой функцией  в это множество попадают все функции вида
в это множество попадают все функции вида  .
.
Покажем, что сумма функций  суммируема с квадратом.
суммируема с квадратом.

Теорема доказана.
Сформулируем и докажем интегральное неравенство Коши-Буняковского (Шварца).
Теорема 3.2.4. Если  , то
, то
 .
.
Доказательство. Для произвольного  и произвольно фиксированных
и произвольно фиксированных  рассмотрим интеграл
рассмотрим интеграл
 .
.
Так как квадратный трехчлен относительно  в правой части неравенства является знакопостоянным, то можно сделать вывод, что дискриминант квадратного трехчлена не превосходит нуля, т.е.
в правой части неравенства является знакопостоянным, то можно сделать вывод, что дискриминант квадратного трехчлена не превосходит нуля, т.е.
 .
.
Иными словами,  .
.
Извлекая корень из обеих частей неравенства, и учитывая, что модуль любого действительного числа не превосходит самого числа, получаем требуемое неравенство.
Теорема доказана.
Аналогично множеству 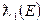 вместо множества
вместо множества  будем рассматривать пространство классов эквивалентных функций
будем рассматривать пространство классов эквивалентных функций  , которое становится нормированным пространством, при определении нормы равенством
, которое становится нормированным пространством, при определении нормы равенством
 . (.2.2)
. (.2.2)
Справедливость аксиом положительной определенности и однородности очевидна. Для доказательства неравенства треугольника используем неравенство Коши-Буняковского.

Справедлива
Теорема 4.2.5. Пространство  является банаховым.
является банаховым.
Кроме того, на пространстве  можно определить скалярное произведение функций
можно определить скалярное произведение функций
 (4.2.3)
(4.2.3)
При этом скалярное произведение (3.2.3) согласовано с нормой (4.2.2) пространства 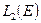 . Иными словами, пространство
. Иными словами, пространство  является гильбертовым.
является гильбертовым.
Дата добавления: 2015-10-30; просмотров: 261 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интеграл Лебега от произвольной измеримой функции. | | | Пространство функций, суммируемых со степенью p. |