Упражнения к главе 1.

1. Определить меру множества .
2. Доказать утверждение теоремы 1.2.2.
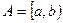3. Пусть и 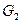- ограниченные открытые множества. Доказать, что если , то .
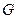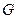4. Доказать, что если ограниченное, открытое множество является объединением конечного или счетного множества открытых множеств , то множество измеримо и .
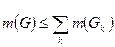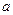5. Пусть - произвольное число такое, что 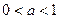. Построим множество с помощью счетного числа шагов следующим образом. На первом шаге удалим из отрезка интервал 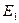длины , расположенный симметрично относительно середины отрезка (назовем такой интервал средним интервалом). На втором шаге из оставшихся двух равных отрезков удалим средние интервалы длины 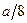каждый. Обозначим объединение этих интервалов . На третьем шаге из оставшихся четырех равных отрезков удалим средние интервалы длины 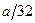. Обозначим объединение этих интервалов .

Обозначим и .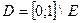

Найти меру множества .

1. Опишем процедуру построения Канторова множества. Построим множество с помощью счетного числа шагов следующим образом. На первом шаге удалим из отрезка интервал 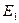длины 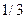, расположенный симметрично относительно середины отрезка (назовем такой интервал средним интервалом). На втором шаге из оставшихся двух равных отрезков удалим средние интервалы длины каждый. Обозначим объединение этих интервалов . На третьем шаге из оставшихся четырех равных отрезков удалим средние интервалы длины 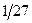. Обозначим объединение этих интервалов . Обозначим . Множе6ство 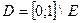называется Канторовым множеством. Найти меру множества .
2. Доказать утверждение теоремы 1.2.1.
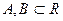3. Доказать, что если - измеримые множества и 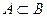, то множество измеримо и

.

1. Доказать, что пересечение конечного или счетного числа измеримых множеств измеримо.
2. Доказать, что разность двух измеримых множеств есть измеримое множество.
3. Доказать, что всякое подмножество множества нулевой меры имеет меру нуль.
4. Может ли равняться нулю мера множества имеющего хотя бы одну внутреннюю точку.
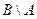5. Доказать, что любое подмножество множества нулевой меры измеримо и имеет нулевую меру.
6. Пусть и - измеримые множества. Доказать равенство

.

1. Доказать, что любое ограниченное измеримое множество , такое что содержит измеримое подмножество меры 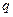, где 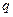- произвольное заданное положительное число меньше .
2. Привести пример не измеримого множества.
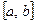3. Доказать, что множество всех рациональных чисел произвольного отрезка имеет нулевую меру.

Дата добавления: 2015-10-30