Мера Лебега ограниченных множеств на числовой прямой.

Мера Лебега числового множества является обобщением понятия длины промежутка числовой оси. При определении меры Лебега будем руководствоваться тем принципом, что введенная мера множества, в частном случае, когда множество является интервалом, должна совпадать с такой характеристикой интервала как длина.

Процедуру определения меры Лебега начнем с определения меры множества, имеющего наиболее простую структуру - открытого множества.

Определение 1.2.1. Мерой интервала 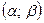называется число 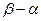, т.е. .

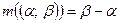Определение 1.2.2. Мерой непустого ограниченного открытого множества 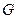называется число, равно сумме длин всех составляющих интервалов множества 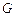, т.е.

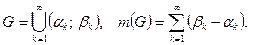
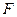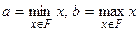Согласно теореме 1.1.2, любое замкнутое множество имеет представление , где , а 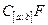- открытое множество.

Определение 1.2.3. Мерой непустого ограниченного замкнутого множества называется число

.

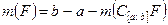Перейдем к построению меры Лебега произвольного ограниченного множества на прямой. С этой целью определим понятия внешней и внутренней меры множества.

Определение 1.2.4. Внешней мерой 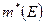ограниченного множества 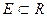называется точная нижняя грань мер всевозможных открытых ограниченных множеств, содержащих множество , т.е.

.

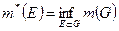Отметим, что в силу ограниченности множества , внешняя мера множества всегда существует и принимает конечное значение .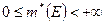

Определение 1.2.5. Внутренней мерой 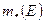ограниченного множества 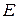называется точная верхняя грань мер всевозможных замкнутых множеств, содержащихся во множестве , т. е

.

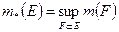Справедливы

Теорема 1.2.1. Есл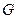и и 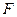- произвольные открытое и замкнутое множества соответственно, то

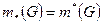и .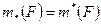

Для всякого ограниченного множества справедливо неравенство .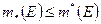

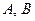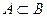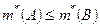Теорема 1.2.2. Если - ограниченные множества и , то и .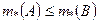

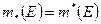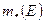Определение 1.2.6. Если для ограниченного множества справедливо равенство , то говорят, что множество измеримо по Лебегу, а общее значение и 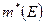называется мерой Лебега множества .

Из определения 1.2.6 и теоремы 1.2.1 следует, что

1) всякое ограниченное открытое множество измеримо и его мера совпадает с мерой, предложенной в определении 1.2.2;

2) всякое ограниченное замкнутое множество измеримо по Лебегу и его мера совпадает с мерой введенной в определении 1.2.3.

Дата добавления: 2015-10-30