Интеграл Лебега от произвольной измеримой функции.

В этом пункте понятие интеграла Лебега будет обобщено на случай произвольной измеримой функции, т.е. неограниченной функции произвольного знака.

С этой целью измеримую функцию представим в виде разности функций

Построенные функции 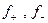являются измеримыми, неотрицательными функциями. Следовательно, они интегрируемы по Лебегу.

Определение 3.4.1. Интегралом Лебега от произвольной измеримой функции назовем число, равное разности интегралов Лебега от функций 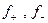, если хотя бы один из них конечен.

Очевидно, что последнее определение интеграла Лебега в случае ограниченной функции совпадает с определением 3.1.1, в случае неотрицательной функции последнее определение интеграла Лебега совпадает с определением 3.3.2.

Таким образом, каждой измеримой функции можно поставить в соответствие число – интеграл Лебега. При этом интеграл Лебега может принимать как конечные значения, так и быть равным несобственным числам .

Определение 3.4.2. Функция называется суммируемой на множестве , если .

Можно показать, что интеграл Лебега от произвольной неограниченной функции обладает всеми свойствами интеграла от ограниченной функции (см. п. 2.4).

В дополнение отметим, что если функция суммируема, то она почти всюду конечна, т.е. 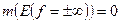. Действительно, достаточно рассуждать о неотрицательной функции. Предположим противное, т.е. , тогда последовательность удовлетворяет неравенству и потому является бесконечно большой, что противоречит условию суммируемости функции.

Кроме того, функция суммируема тогда и только тогда, когда суммируема функция . Поэтому условие в определении 3.4.2 суммируемой функции можно заменить условием .

В связи с последним замечанием, отметим, что интеграл Римана этим свойством не обладает, достаточно привести пример неограниченной функции, несобственный интеграл которой является сходящимся не абсолютно.

В заключении отметим, что любая интегрируемая по Риману на отрезке функция интегрируема по Лебегу, и эти интегралы совпадают

Дата добавления: 2015-10-30