Теорема 3.2.2. (аддитивность относительно области интегрирования).

Если измеримое множество есть объединение конечного или счетного числа попарно не пересекающихся измеримых множеств и функция определена и интегрируема на каждом из них, то она интегрируема на , причем

.

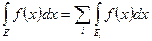Доказательство. Покажем справедливость теоремы для случая . Построим интегральную сумму Лебега на множестве . Обозначим

, , .

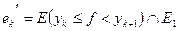Очевидно, что 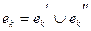. Отсюда

.

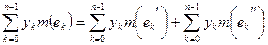Переходя к пределу при получаем

.

Используя метод математической индукции, полученный результат легко обобщить на случай конечного числа множеств . Покажем справедливость утверждения теоремы для счетного числа множеств, т.е. для случая, когда 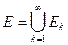. Справедливо равенство . Так как множество 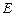измеримо, то ряд в правой части последнего равенства сходится, поэтому . Положим . Тогда

.

Для последнего слагаемого применим теорему о среднем

.

Но так как , то 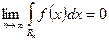. Поэтому

.

Теорема доказана.

Следствие 3.2.4. Если - измеримые ограниченные функции эквивалентные между собой, то .

Доказательство. Множество представим в виде объединения . Тогда

.

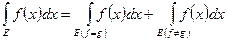Так как 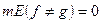, то .

.

Следствие доказано.

Следствие 3.2.5. Интеграл от функции эквивалентной нулю равен нулю.

Следствие 3.2.6. Если - измеримая ограниченная неотрицательная функция, такая ч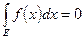то , то эквивалентна нулевой функции.

Теорема 3.2.3. Интегрирование по Лебегу является линейной операцией, т.е. если - интегрируемые по Лебегу функции и - произвольные скаляры, то функция интегрируема по Лебегу, причем

.

Справедливость утверждения теоремы обусловлена тем фактом, что операции суммирования и предельного перехода являются линейными.

Теорема 3.2.4. Если интегрируема по Лебегу на множестве , то

.

Доказательство. Положим , . Тогда

.

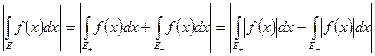С другой стороны .

В силу неравенства при , имеем .

Теорема доказана.

Теорема 3.2.5. (о предельном переходе под знаком интеграла). Пусть - последовательность, интегрируемых по Лебегу на множестве , функций, сходящаяся по мере к измеримой ограниченной функции . Если существует такая постоянная , что для любого и произвольного справедливо неравенство , то .

Теорема 3.2.6. (сравнение интеграла Римана и интеграла Лебега). Всякая функция, интегрируемая по Риману, является интегрируемой по Лебегу.

Пример функции Дирихле показывает, что обратное утверждение не верно.

Дата добавления: 2015-10-30