Вспомогательные определения и утверждения.

Мера Лебега. Интеграл Лебега. Пространства суммируемых по Лебегу функций.

С О Д Е Р Ж А Н И Е

Глава 1. Мера Лебега.

1.0. Вспомогательные определения и утверждения.

1.1. Структура открытых и замкнутых множеств на числовой прямой.

1.2. Мера Лебега ограниченных множеств на числовой прямой.

1.3. Свойства измеримых по Лебегу множеств.

1.4. Классы измеримых множеств.

Упражнения к главе 1.

Глава 2. Измеримые функции.

2.1. Измеримые функции.

2.2. Свойства измеримых функций.

2.3. Последовательности измеримых функций.

Упражнения к главе 2.

Глава 3. Интеграл Лебега.

3.1. Интеграл Лебега от ограниченной функции. Свойства интеграла Лебега.

3.2. Интеграл Лебега от неограниченной неотрицательной функции.

3.3. Интеграл Лебега от произвольной измеримой функции.

Упражнения к главе 3.

Глава 4. Суммируемые функции.

4.1. Пространство суммируемых функций.

4.2. Пространство суммируемых с квадратом функций.

4.3. Пространство .

Упражнения к главе 4.

Глава 1. Мера Лебега.

Вспомогательные определения и утверждения.

В этом параграфе мы приведем необходимые для дальнейшего изложения понятия о множествах являющихся подмножествами множества действительных чисел 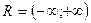(так называемые линейные множества).

В частности нам потребуется понятия открытого и замкнутого множества. В топологии понятие открытого множества вводится аксиоматически. Однако, учитывая простоту рассматриваемых множеств, в изложении мы будем избегать аксиоматического определения открытых множеств.

Элементами рассматриваемых множеств являются числа, поэтому не возникает недоразумений при отождествлении элемента с точкой на числовой оси, имеющей координату .

Множества

, , ,

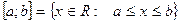будем называть соответственно отрезком, интервалом, полуинтервалом с включенным левым концом, полуинтервалом с включенным правым концом.

Для элемента 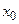интервал вида 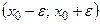будем называть -окрестностью элемента и обозначать .

Точка 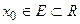называется внутренней точкой множества, если существует -окрестность элемента принадлежащая множеству .

Множество 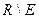называется дополнением множества .

Множество , имеющее открытое дополнение называется замкнутым.

Утверждение 1. Объединение открытых множеств является открытым множеством. Пересечение конечного числа открытых множеств есть открытое множество.

Утверждение 2. Объединение конечного числа замкнутых множеств, является замкнутым множеством, пересечение любого числа замкнутых множеств есть замкнутое множество.

Точной нижней гранью множества называется такое число , что

1) для любого справедливо неравенство ;

2) для любого 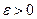найдется такой элемент , что .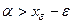

Точную нижнюю грань множества будем обозначать .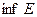

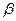Точной верхней гранью множества называется такое число , что

1) для любого справедливо неравенство ;

2) для любого 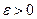найдется такой элемент , что .

Точную верхнюю грань множества будем обозначать .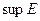

Для любого замкнутого числового множества . Поэтому точные нижнюю и верхнюю грани замкнутого множества будем обозначать соответственно .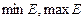

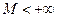Множество называется ограниченным, если найдется такое число , что .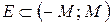

Символом 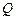будем обозначать множество рациональных чисел.

Дата добавления: 2015-10-30