Уравнение неразрывности трехмерного потока

Для решения задач гидродинамики нужно уметь определять в любой точке потока направление и величину скорости движения жидкости или три ее проекции (u_x, u_y, u_z) и давление р. Неизвестных, таким образом, получается четыре, и трех уравнений движения (уравнений Эйлера для идеальной жидкости или уравнений Навье – Стокса для вязкой) недостаточно для решения этой задачи.

Необходимое для решения основной задачи четвертое уравнение может быть выведено исходя из условия неразрывности потока.

Но прежде чем приступить к выводу данного уравнения, рассмот­рим вспомогательный вопрос о вычислении расхода жидкости через произвольное бесконечно малое сечение потока.

Расходом называется количество жидкости, протекающее за едини­цу времени через рассматриваемое сечение потока. Он может измеря­ться в единицах массы – массовый расход (M, кг/с), веса – весовой расход (G, Н/с) или в единицах объема – объемный расход (Q, м³/с).

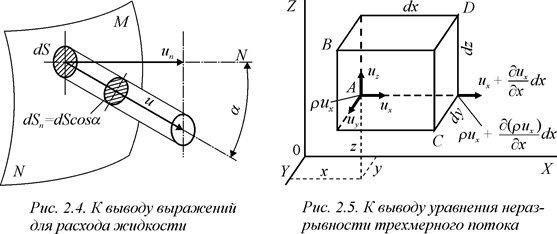
Пусть в некоторой точке А произвольного сечения потока жидко­сти, ограниченного поверхностью МN, вектор скорости имеет в данный момент времени величину u, а его направление определяется углом a к нормали, проведенной через рассматриваемую точку сечения (рис. 2.4). Если возле этой точки на поверхности сечения выделить элементарную площадку dS, то проходящие через нее в единицу времени частицы составят объем наклонного цилиндра, основанием которого является эта площадка, а длиной – вектор скорости (путь, пройденный каждой частицей в единицу времени).

Так как dS_n = dS cosa – нормальное сечение цилиндра, то объем его можно выразить следующим образом:

dQ = udS cosa, м³/с.

Но u cosa = u_n – нормальная к плоскости сечения составляющая произ­вольно направленной скорости u в данной точке. Поэтому

dQ = u_n dS.

Масса жидкости, имеющей плотность r и проходящей через площадку dS в единицу времени, должна быть выражена как

dM = r u_n dS.

Эти выражения определяют расход жидкости (объемный dQ и массовый dM) через произвольное бесконечно малое сечение потока.

Чтобы установить зависимость, выражающую условие неразрывно­сти в общем виде, выделим возле рассматриваемой точки А (х, у, z) бес­конечно малый прямоугольный параллелепипед ABCD, ребра которого параллельны координатным осям (рис. 2.5). Скорость в этой точке u, ее составляющие по осям – u_x, u_y, u_z. Через грань АВ, площадь которой dS_x = dydz, в объем параллелепипеда за счет движения вдоль оси Ох за время dt втекает масса жидкости dm = dMdt = r u_x dydzdt. На расстоя­нии dx от точки А составляющая скорости u_x изменяется на (¶ u_x/ ¶ x) dx. В других вершинах рассматриваемого параллелепипеда составляющие скорости имеют соответствующие приращения.

Плотность жидкости в общем случае также переменная величина и на том же расстоянии dx может иметь приращение (¶r / ¶ x) dx. Измене­ние произведения r u_x на длине dx следует, поэтому выразить как

.

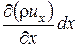В соответствии с этим масса жидкости, вытекающей за тот же отрезок времени dt через противоположную грань CD параллелепипеда за счет движения вдоль оси Ох, определяется выражением

.

Изменение массы жидкости в объеме параллелепипеда за счет движения вдоль оси Ox будет

.

Так же выражаем изменение массы в объеме параллелепипеда за счет движения вдоль двух других координатных осей

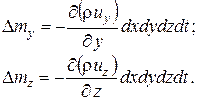
Получаем общее изменение массы жидкости в объеме параллеле­пипеда за время dt за счет движения частиц жидкости со скоростью u:

.

За тот же отрезок времени плотность жидкости в объеме паралле­лепипеда могла измениться на величину – (¶r / ¶ t) dt. Поэтому масса жидкости в объеме параллелепипеда АВCD по истечении времени dt будет составлять величину

,

а изменение массы жидкости в этом объеме за данный отрезок време­ни вследствие изменения плотности будет

D m _r = (¶r/¶t) dxdydzdt.

Если поток неразрывен, то изменение массы в рассматриваемом объеме вследствие движения жидкости должно компенсироваться соответствующим изменением плотности, т. е. выполняться условие

D m_u = D m _r .

После подстановки и сокращения на dxdydzdt получим общее выражение условия неразрывности для трехмерного потока в виде

. (2.7)

В такой форме уравнение неразрывности справедливо как для несжимаемой, так и для сжимаемой жидкости (газа).

Для несжимаемой жидкости

r = const; ¶r/¶ t = 0

и уравнение неразрывности упрощается

. (2.7а)

* * *

Таким образом, в §2:

– Даны определения вихря, потенциала скорости, расхода жидкости.

– Приведена формулировка теоремы Гельмгольца – Коши

– Выведены уравнения для составляющих угловой скорости вращения жидкой частицы.

– Получено выражение, определяющее условие существования потен­циального движения жидкости.

– Выведены дифференциальные уравнения движения идеальной жид­кости (Эйлера) и вязкой (Навье–Стокса), а также уравнение нераз­рывности трехмерного потока.

Вопросы и задачи

1. Сформулируйте теорему Геймгольца–Коши.

2. Приведите выражения для составляющих угловой скорости вращения жидкой частицы. Сформулируйте понятия вихревого и потенциального движения жид­кой частицы. Напишите выражение для потенциала скорости.

3. Приведите системы дифференциальных уравнений движения идеальной и вяз­кой жидкостей. Раскройте физический смысл членов этих уравнений.

4. Приведите выражение условия неразрывности трехмерного потока сжимаемой жидкости. Какой вид оно приобретает в случае, если жидкость несжимаема?

Задача. Получить выражение для скорости слоистого плоскопараллельного стационарного течения жидкости в канале, ограниченном двумя параллельными плоскими стенками, если расстояние от оси канала до стенок равно b.

Ответ: .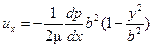

Решение. Отличительным признаком слоистого течения является отсутствие в уравнении Навье–Стокса инерционных членов, т.е. наличие только одной состав­ляющей скорости. Если этой составляющей является скорость u_x (т.е. движение идет в направлении оси х), а составляющие u_y и u_z равны нулю, то из уравнения неразрывности следует, что ¶ u_x /¶ x = 0 и, следовательно, u_x от координаты x не зависит. Таким образом, для слоистого течения имеем u _x= u _x(y, z); u_y = 0; u_z = 0; ¶ p /¶ y = 0, ¶ p /¶ z = 0, и вместо полной системы (2.6) получим для стационарного течения линейное дифференциальное уравнение относительно скорости u_x (y, z)

. (а)

Заметим, что, поскольку в этом соотношении слева стоит функция координат x, а справа – функция координат y и z, то dp / dx = const.

Плоскопараллельное течение в канале, ограниченном двумя парал­лельными плоскими стенками скорость u_x, к тому же не зависит от координаты z и уравнение (а) принимает вид dp / dx = m d ² u_x / dy ². Его интегрирование дает

,

где С ₁ и С ₂ – постоянные интегрирования, для определения которых имеются два условии: а) при y = + b u = 0; б) при y = – b u = 0.

В результате С ₁ = 0, и искомое выражение для скорости привет вид

.

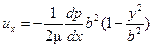Дата добавления: 2015-10-29