Элементарная струйка потока. Уравнение неразрывности для элементарной струйки при установившемся движении

Решение основных вопросов гидрогазодинамики упрощается, если рассматривать одномерное движение жидкости. Для исследования по­тока жидкости конечных размеров с позиций одномерного движения в прикладной гидравлике пользуются гипотезой о струйной модели дви­жения жидкости. Считается, что поток состоит из бесконечно большо­го числа отдельных элементарных струек, поперечные сечения кото­рых бесконечно малы. Поэтому все параметры движения в пределах какого-либо сечения элементарной струйки dS можно принять неизменными. Рассмотрим ее свойства.

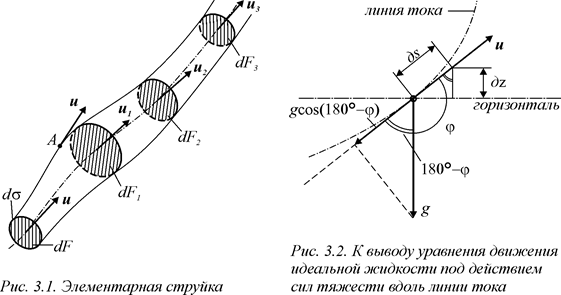
Если в потоке жидкости выделить произвольный, бесконечно малый контур d s и через все его точки провести линии тока (рис. 3.1), они образуют собой трубчатую поверхность, называемую трубкой тока. Совокупность линий тока, проведенных через все точки сечения dS, ограниченного элементарным контуром d s, или часть потока, ограниченная трубкой тока, называется элементарной струйкой. Под сечением элементарной струйки понимают при этом ограниченную ею часть поверхности, нормальную к направлению скорости.

Так как сечения элементарной струйки бесконечно малы, скорость во всех точках каждого из них считается одинаковой по величине и направлению, а сами сечения – плоскими. На протяжении элементар­ной струйки площади ее сечений могут изменяться (dS ₁ ¹ dS ₂ ¹ dS ₃), так как форма линий тока, их ограничивающих, может быть произвольной. В каждом из таких сечений имеется своя скорость u ₁, u ₂, u ₃ и т. д.

Элементарная струйка обладает следующими свойствами:

1) при установившемся движении она не меняет своей формы;

2) ни одна частица жидкости не может проникать через ее боковую поверхность, что вытекает из определения линии тока.

В любой точке (например, в точке А на рис. 3.1) боковой поверх­ности струйки, скорость может быть направлена только по касательной к этой поверхности; нормальных к поверхности составляющих скорости не существует.

Элементарная струйка является, таким образом, вполне самостоятельным (изолированным) элементом потока, а ее воображаемая боковая поверхность – непроницаемой.

Величины х, у, z, и, р,r, входящие в основные уравнения гидрогазо­динамики, считаются, с точностью до бесконечно малой величины, одинаковыми во всех точках любого из сечений элементарной струйки.

Поэтому, рассматривая движение частицы жидкости вдоль какой-либо линии тока данной элементарной струйки, все законы ее движения можно распространять и на всю элементарную струйку.

Движение потока в целом можно рассматривать как совокупность движений отдельных струек. Но в сечении потока конечных размеров интересующие нас величины могут заметно изменяться при переходе из одной точки в другую, от одной элементарной струйки к другой. Элементарные струйки при этом как бы скользят друг по другу.

При одномерном установившемся движении частицы жидкости вдоль линии тока, ее положение, а, следовательно, скорость и давление в какой-либо точке пространства вполне определяются путем s, прой­денным от некоторого начального положения, т. е.

u = f (s); p=f (s).

При этом, как отмечалось выше, направление скорости в каждой точке определяется касательной к линии тока, и нас интересует, по сути дела, только ее величина (модуль вектора). Нет поэтому необхо­димости учитывать здесь отдельные составляющие вектора скорости по координатным осям.

Выведем уравнение неразрывности или расхода для элементарной струйки при установившемся движении.

Для этого рассмотрим отсек элементарной струйки между двумя произвольными сечениями dS ₁ и dS ₂, скорости в которых соответствен­но u ₁ и u ₂, а плотность жидкости r₁ и r₂ (рис. 3.1).

За время dt в рассматриваемый отсек струйки через сечение dS ₁ втекает масса жидкости dm ₁

dm₁ = r₁u₁dS₁dt,

а через сечение dS ₂ за то же время вытекает масса жидкости dm ₂

dm ₂ = r₂ u ₂ dS ₂ dt.

Так как при установившемся движении форма и объем рассматри­ваемого отсека не изменяются, плотность жидкости в каждой точке сечения, а, следовательно, и средняя плотность по всему отсеку также не изменяются. Притока и оттока жидкости через боковую поверхность струйки не существует. Поэтому из условия неразрывности следует, что масса втекающей жидкости dm ₁ и вытекающая – dm ₂ равны, т. е.

r₁ u ₁ dS ₁ dt = r₂ u ₂ dS ₂ dt.

Сокращая на dt и учитывая произвольность выбора сечения, получим

r₁ u ₁ dS ₁ = r₂ u ₂ dS ₂ = r udS = dM = const, (3.1)

т.е. массовый расход жидкости при установившемся движении одинаков во всех сечениях элементарной струйки.

Уравнение неразрывности (3.1), записанное в единицах массового расхода, пригодно как для несжимаемой жидкости, так и для газа.

Для газового потока удобнее записать уравнение неразрывности в весовых единицах. Такое уравнение получается, если умножить уравне­ние (3.1) на g = const. Так как r g = g, то

g₁u₁dS₁ = g₂u₂dS₂ = …= gudS = dG = const. (3.1 а)

Для несжимаемой жидкости r = const; поэтому, учитывая, что udS = dQ – объемный расход, получим следующие уравнение неразрыв­ности в объемных единицах для несжимаемой жидкости:

u ₁ dS ₁ = u ₂ dS ₂ = udS = dQ = const. (3.1 б)

Из этого уравнения следует, что u ₂/ u ₁ = dS ₁/ dS ₂, т.е. площадь сече­ния струйки для несжимаемой жидкости обратно-пропорциональна скорости.

Дата добавления: 2015-10-29