Уравнение Бернулли (энергии) для газа

Уравнение (3.6) после сокращения на ds имеет вид

gdz + dp /r + d (u ²/2) = 0. (4.9)

Так как для сжимаемой жидкости r ¹ const, то во втором члене этого уравнения появляется вторая переменная. Интегрируя уравнение (4.9) вдоль элементарной струйки от сечения 1 до сечения 2 (т.е. в пределах от z ₁, p ₁, u ₁, и r₁ до z ₂, p ₂, u ₂, и r₂), получим

, (4.10)

что является уравнением Бернулли для газа в механической форме.

Величину интеграла, стоящего в левой части этого уравнения, можно найти, если плотность является функцией от давления. Вид этой функции зависит от термодинамического процесса, происходящего в том или другом случае движения газа.

Рассмотрим установившееся одномерное движение газа под действием силы тяжести.

Из-за малой плотности газа можно пренебречь в уравнении (4.10) членом (z ₂ - z ₁) g, так как для газа сила веса пренебрежимо мала по сравнению с силами инерции и давления. Тогда получаем уравнение:

. (4.11)

Считая течение адиабатическим, выразим в последнем уравнении отношение dp /r с помощью выражений (4.6):

dp /r = kC r ^{k – 2} d r.

Подставляя найденное выражение в уравнение (4.11) и интегрируя, получим уравнение энергии в интегральной форме или уравнение Бернулли – Сен-Венана (1839):

или . (4.12)

Либо, разделив члены уравнения (4.12) на g, имеем:

. (4.12а)

Сравнивая выражение (4.12а) с уравнением Бернулли для идеальной несжимаемой жидкости (3.7), видим, что отличие состоит в множителе k/ (k – 1) при пьезометрической высоте p /g. Появление этого множителя связано с тем, что в потенциальную энергию газа входит еще и его внутренняя энергия. Иногда говорят, что в случае газа к пьезометрическому напору добавляется "температурный напор".

Выражая в уравнении энергии (4.12) отношение p /r через уравне­ние состояния (4.2), получим

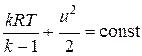. (4.12б)

Последнее равенство показывает, что при отсутствии теплообмена с внешней средой увеличение скорости вдоль струйки приводит к падению температуры газа и наоборот.

Используя формулу для скорости звука (4.7а), уравнение энергии (4.12б) можно представить в виде:

, (4.12в)

откуда ясно, что скорость движения газа и скорость звука взаимосвяза­ны: Увеличение скорости течения приводит к уменьшению скорости звука. Вследствие адиабатного охлаждения она меньше скорости звука, соответствующей начальному состоянию газа, когда скорость равна нулю и температура наибольшая.

Выражение (4.12в) позволяет выяснить смысл постоянной в правой части уравнения энергии. Действительно, в покоящемся газе u = 0 и скорость звука достигает своей наибольшей величины a ₀. Следовательно, const = a ₀²/(k – 1) и уравнение энергии может быть представлено в виде:

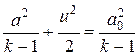, (4.12г)

Наконец, если использовать понятие энтальпии, или теплосодер­жания газа i, рассматриваемое в термодинамике:

,

то уравнение энергии (4.12б) примет вид:

i + u ²/2 = const. (4.12д)

Таким образом, потенциальная энергия газа выражается в различ­ных формах уравнения энергии (3.25)–(3.25д) с помощью различных параметров – давления, температуры, скорости звука, энтальпии.

Отметим, что для реального газа, также как и для реальной несжи­маемой жидкости, необходимо учесть потери энергии на сопротивле­ние, добавив в левую часть уравнений энергии слагаемое h_u.

Дата добавления: 2015-10-29