Неустановившееся движение идеальной жидкости под действием сил тяжести вдоль линии тока

Если бесконечно малый отрезок пути, проходимого частицей за бесконечно малый отрезок времени вдоль линии тока, обозначить ds, а проекцию ускорения массовых сил, действующих на движущуюся жидкую частицу, на направление касательной к линии тока в рассмат­риваемой точке – X_s, то уравнение Эйлера запишется в виде:

. (3.2)

Математические трудности не позволяют проинтегрировать это дифференциальное уравнение в общей форме и найти тем самым функ­циональные зависимости:

u = f (t, s) и p = φ (t, s)

т. е. решить основную задачу гидрогазодинамики для одномерного движения под действием массовых сил любой природы.

В случае, когда движение жидкости происходит под действием только сил тяжести, направленных всегда вертикально вниз, такая задача решается просто. Проекцию ускорения массовых сил g на направление движения в этом случае (рис. 3.2) можно выразить как

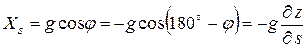. (3.3)

где ∂s и ∂z – частные приращения пути s и высоты z при неустановив­шемся движении по линии тока.

Полная производная du/dt в уравнение (3.2), с учетом того, что полный дифференциал u равен du = (¶ u /¶ t) dt + (¶ u /¶ s) ds, имеет вид

. (3.4)

Подставляя выражения для X_s и du/dt из уравнений (3.3) и (3.4) в уравнение (3.2), получим

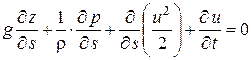. (3.5)

Дифференциальное уравнение (3.5) является уравнением неустановив­шегося движения жидкости как несжимаемой, так и газообразной.

Для несжимаемой жидкости r = const. Поэтому второй член уравнения можно представить как

.

Интересующее нас уравнение неустановившегося движения для несжимаемой жидкости можно теперь записать в виде

(3.5 а)

Величины, входящие в трехчлен в квадратных скобках (называе­мый обычно трехчленом Бернулли) в системе СИ имеют размерность Дж/кг и несут в себе следующий энергетический смысл:

gz – потенциальная энергия единицы массы (удельная) частицы жидкости, находящейся на высоте z от плоскости сравнения;

p/r – удельная потенциальная энергия давлением на жидкую частицу;

u ²/2 – удельная кинетическая энергия частицы жидкости.

Проинтегрировав выражение (3.5 а) получим׃

, (3.5 б)

Величина , в случае, если бы движение шло по линии тока (что возможно лишь при установившемся движении), определяла бы удельную работу сил инерции на пути s. Так как при неустановившем­ся движении частицы жидкости движутся по траектории, которая не совпадает с линией тока, то, строго говоря, так определять величину данного слагаемого нельзя, но приведенное разъяснение помогает понять ее физический смысл.

Чтобы проинтегрировать выражение , надо знать Практически это редко известно. Поэтому в прикладной гидравлике рассматривают обычно установившееся движение, так как описываю­щие его уравнения имеют удобную для интегрирования форму.

Дата добавления: 2015-10-29