Связи скорости газа с сечением потока. Сопло Лаваля

Выясним зависимость скорости течения газа от площади попереч­ного сечения потока. Для газа уравнение неразрывности при устано­вившемся течении, имеет вид:

r uS = const. (4.13)

Логарифмируя и дифференцируя это равенство, получим

d r/r + du / u + dS / S = 0, (4.13a)

откуда

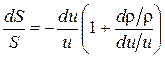. (4.13б)

Из уравнения (4.9), пренебрегая энергией положения (gdz = 0), имеем

,

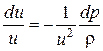что дает после подставки в уравнение (4.13б)

.

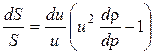Поскольку согласно формуле (4.5) dp / d r = a ², имеем

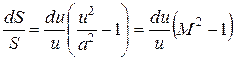. (4.14)

Из уравнения (4.14) следует, что изменение скорости du при изменение сечения dS происходит по-разному для дозвукового и сверхзвукового течения.

В дозвуковом потоке (u < a, Μ < 1, рис. 4.1а) знаки du и dS в (4.14) противоположны: уменьшение сечения в конфузорном канале приво­дит к возрастанию скорости, а в диффузорном канале скорость по по­току уменьшается. При сверхзвуковом течении u > a, Μ > 1, (рис. 4.1б) в конфузорном канале поток замедляется, в диффузорном – ускоряется.

Чтобы пояснить результаты, полученные для сверхзвукового течения, сопоставим уравнения (4.14) и (4.13б). Имеем

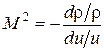. (4.15)

Поскольку левая часть равенства (4.15) всегда положительна, ясно, что знаки dρ и du всегда противоположны: рост скорости приводит к

уменьшению плотности. Но при дозвуковом течении (M ² < 1) скорость изменяется более быстро, чем плотность:

du / u > d r/r.

При сверхзвуковом течении, наоборот, более быстро уменьшается плотность:

du / u < d r/r.

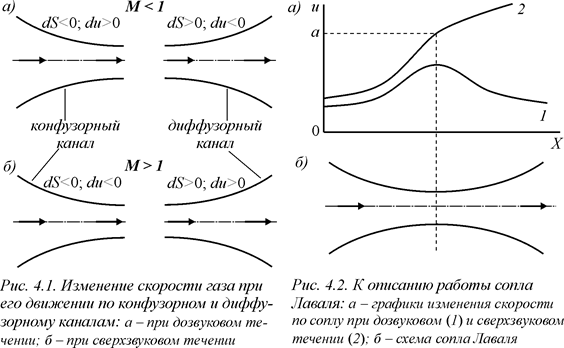
Для получения сверхзвуковых скоростей газа в технике использует­ся сопло Лаваля (1889, рис. 4.2), принцип действия которого ясен из приведенных рассуждений. В дозвуковом потоке, поступающем в суживающуюся часть сопла Лаваля, скорость увеличивается. Если в наименьшем сечении сопла не достигается скорость, равная скорости звука, то в расширяющейся части происходит ее уменьшение (кривая 1 на рис. 4.2). Если перепад давления достаточно велик, чтобы в наименьшем сечении скорость течения сравнялась со скоростью звука, то при дальнейшем расширении поток переходит в сверхзвуковой (кривая 2 на рис.4.2)

Сопло Лаваля имеет широкое применение, являясь составной частью реактивных двигателей, сопловых аппаратов некоторых турбин (в которых рабочие лопатки обтекаются сверхзвуковым потоком), сверхзвуковых аэродинамических труб и. т. д.

* * *

Таким образом, в §4:

– Рассмотрены соотношения термодинамики, связывающие основные параметры состояния газа.

– Приведены выражения для скорости звука и числа Маха.

– Выведены основные уравнения, описывающие одномерное движение газа: уравнения Бернулли (энергии) в различных формах и уравнение неразрывности, связывающее скорость газа с сечением потока.

– Описаны устройство и принцип работы сопла Лаваля.

Вопросы и задачи

1. Что понимают под уравнением состояния идеального газа? Приведите выраже­ние, связывающее относительную плотность газа по воздуху с газовой постоян­ной данного газа.

2. Какие характерные процессы изменения состояния газа обычно рассматривают в термодинамике? Напишите соотношения, связывающие давление, плотность и температуру при адиабатическом процессе.

3. Приведите выражения для скорости звука и числа Маха? Что это число характе­ризует? Какие виды течения газа Вы знаете?

4. Напишите уравнение Бернулли для газа в интегральной форме. Какие другие варианты записи этого уравнения Вы знаете? Раскройте их физический смысл.

5. Приведите выражение, отражающее связь скорости газа с сечением потока. Как влияет режим течения газа на эту взаимосвязь?

6. Опишите устройство и принцип работы сопла Лаваля. Где оно применяется?

Задача 1. Определить массу 100 тыс. нормальных (т.е. давление атмосферное, t = 20°С) кубометров газа, если его молярная масса m = 19,2 кг/кмоль.

Ответ: 79,842 т.

Задача 2. Давление в газовом резервуаре составляет 0,12 МПа, температура +15°С. На сколько повысится давление в этом резервуаре, если температура в нем возрастает на 15°С?

Ответ: 6,3 кПа

Задача 3. При стационарной перекачки газа давление и температура в начале участка газопровода составляет 5,2 МПа и 35°С, а в его конце 3,5 МПа и 10°С, соответственно. Определить, пренебрегая сжимаемостью газа, во сколько раз скорость газа в конце участка превышает скорость газа в его начале.

Ответ: В 1,365 раза.

Дата добавления: 2015-10-29