Установившееся движение идеальной жидкости. Уравнение Бернулли

При установившемся движении скорость и давление от времени не зависят и являются в случае одномерного движения функциями только одной переменной – пути s:

u = f (s); р = φ (s).

Поэтому дифференциальное уравнение (3.5) при установившемся дви­жении идеальной жидкости для частицы, движущейся под действием сил тяжести вдоль линии тока, в общем виде может быть записано так:

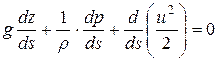, (3.6)

Интегрирование этого уравнения удобнее рассмотреть для несжимае­мой жидкости и для газа (см. п. 4.2) отдельно.

Для несжимаемой жидкости r = const. Второй член уравнения (3.6) в этом случае можно представить как

.

С учетом этого и после деления на g уравнение (3.6) принимает вид

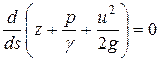
и, следовательно, легко интегрируется:

. (3.7)

Это уравнение называется уравнением Бернулли. Оно служит основой для практического решения подавляющего большинства задач прикладной гидравлики.

Так как в пределах любого из сечений элементарной струйки величины z, p и u с точностью до бесконечно малых могут считаться одинаковыми, уравнение Бернулли (3.7) может быть применено не только к частице жидкости, движущейся вдоль линии тока, но и для всей элементарной струйки в целом.

Члены уравнения (3.7) имеют линейную размерность (м), поэтому можно выявить их геометрический смысл.

Отнесем струйку к системе координат XYZ (рис.3.3 а), и напишем уравнение Бернулли для двух произвольных сечений струйки

. (3.8)

Здесь z – геометрическая высота центра тяжести сечения над плоскостью XOY;

p /g – пьезометрическая высота (высота столба жидкости, создающая своим весом давление р);

u ²/(2 g) – скоростная высота или скоростной напор.

Сумма всех этих величин, обозначаемая через Н, называется полным напором в данном сечении струйки.

Для поперечного сечения элементарной струйки величину Н можно представить совокупность отрезков (z), (p /g) и [ u ²/(2 g)], как на рис.3.3 а.

Соединив между собой концы отрезков Н, получим кривую Е–Е, расположенную в горизонтальной плоскости; эта кривая называется линией полного напора или гидравлической линией.

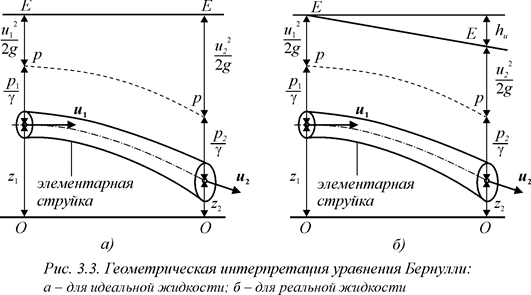
Соединив кривой концы отрезков p /g, получим линию р–р, которую называют пьезометрической линией.

Вернувшись к энергетической интерпретации (умножив уравнение (3.7) на g) легко увидеть, что уравнение Бернулли представляет собой закон сохранения полной удельной механической энергии при устано­вившемся движении несжимаемой идеальной жидкости под действием сил тяжести, так как согласно нему сумма потенциальной энергии (положения и давления) и кинетической есть величина постоянная. Поэтому уравнение Бернулли называют еще уравнением энергии.

3.4. Уравнение Бернулли для потока реальной жидкости

Применяя, уравнение Бернулли к струйке реальной жидкости, необходимо учесть, что полная механическая энергия, не остается постоянной вдоль струйки. Эту потерю механической энергии на участке струйки между двумя сечениями учитывают введением в пра­вую часть уравнения Бернулли (3.8) слагаемого h_u – потери напора (потери удельной механической энергии).

Гидравлическая линия Е–Е (рис. 3.3 б) в этом случае не горизон­тальна и снижается вниз по течению; чем больше наклон, этой линии, тем интенсивнее расходуется энергия по пути.

Безразмерную величину I, определяющую уменьшение напора на единицу длины трубопровода, называют гидравлическим уклоном, т. е.

I = dh _u / dl, (3.9)

где dl – длине рассматриваемого участка струйки; dh _u – потери напора на длине этого участка.

Переходя к потоку жидкости конечных размеров (такому, как в трубе или канале), естественно для расчета скоростного напора исполь­зуют среднюю скорость u _cp. Для определения средней скорости по скоростям отдельных струек используется формула:

.

Следовательно, объемный расход потока жидкости Q = u _ср× S. В свя­зи с этим, условие неразрывности для несжимаемой жидкости примет вид:

Q = u _ср S = const,

а для сжимаемой жидкости:

M = r u _ср S = const или G = g u _ср S = const.

Однако, если скорости струек в сечении неодинаковы (например, замедляются у стенок трубы вследствие трения), то расчет кинетиче­ской энергии по средней скорости u _сp приведет к заниженным резуль­татам по сравнению с расчетом суммарной кинетической энергии отдельных струек. Это происходит потому, что скорость входит в член уравнения, учитывающий кинетическую энергию, в степени выше первой. Такое затруднение преодолевают введением в кинетическую энергию, вычисленную по средней скорости, поправочного коэффициента (коэффициента Кориолиса) α > 1. Очевидно, что α численно равен отношению суммарной кинетической энергии струек к энергии, вычисленной по средней скорости потока. В итоге уравнение Бернулли для вязкой жидкости приобретает вид:

. (3.10)

В дальнейшем, в уравнениях для реальной жидкости, среднюю скорость будем обозначать через u без индекса.

Величина коэффициента α возрастает с ростом поперечной нерав­номерности скоростей в сечении трубы. Для ламинарного течения в круглой трубе α = 2. Для т урбулентного течения, в котором скорости мало меняются по сечению трубы, по опытным данным, α = 1,05 – 1,1.

Рассмотрим вопрос о выборе сечений потока, к которым можно применять уравнение Бернулли. Очевидно, что эти сечения нельзя выбирать в местах резкого поворота потока, так как из-за действия центробежной силы инерции в таком сечении давления распределены неравномерно. Нельзя применять уравнение Бернулли и к сечениям, в которых резко возрастает поперечная неравномерность скоростей, на­пример в зонах расширения потока после диафрагмы, где появляются противотоки и вихревые области. В таких сечениях невозможно дос­таточно точно определить коэффициент неравномерности скоростей α. Расчету таких сечений посвящен §7.

* * *

Таким образом, в §3:

– Рассмотрены основные понятия, позволяющие описать поток жид­кости с позиции прикладной гидравлики: трубка тока, элементарная струйка потока, даны их определения и основные свойства.

– Получены различные формы уравнения неразрывности (расхода) для элементарной струйки при установившемся движении.

– Выведены уравнения Бернулли, описывающие одномерное движение идеальной и реальной жидкостей. Раскрыт энергетический и геоме­трический смысл величин, входящих в данные уравнения.

– Отмечено, что уравнения, использующиеся для описания движения газа, имеют свои особенности и будут описаны ниже.

Вопросы и задачи

1. Сформулируйте гипотезу о струйной модели движения жидкости, используемую в прикладной гидравлике. Приведите понятие и свойства элементарной струйки.

2. Сформулируйте понятие расхода жидкости. Какие виды расходов Вы знаете? Напишите уравнение неразрывности для элементарной струйки при установив­шемся движении в различных формах.

3. Приведите уравнение для неустановившегося движения идеальной сжимаемой жидкости под действием сил тяжести вдоль линии тока. Какой вид оно приобре­тает в случае, если жидкость несжимаема? Раскройте энергетический смысл величин, входящих в трехчлен Бернулли.

4. Напишите уравнение для установившегося движения идеальной несжимаемой жидкости (уравнение Бернулли). Раскройте геометрический смысл величин, входящих в это уравнение.

5. Что такое потери напора? Сформулируйте понятие гидравлического уклона.

6. Что понимают под средней скоростью движения жидкости? Раскройте физичес­кий смысл коэффициента Кориолиса. Приведите его значения для ламинарного и турбулентного течения жидкости. Напишите уравнение Бернулли для потока реальной жидкости.

Задача 1. Средняя по сечению скорость u течения вязкой жидкости (ρ = = 900 кг/м³) в трубопроводе с внешним диаметром D = 1020 мм и толщиной стенки δ = 10 мм, равна 1,0 м/с. Определить массовый расход трубопровода за год.

Ответ: 21,365млн. т/год

Примечание: Число рабочих дней принять равным 350.

Задача 2. Трубопровод состоит из двух последовательно соединенных участ­ков: первого – с внешним диаметром D ₁ = 530 мм и толщиной стенки δ = 8 мм, и второго с диаметром D ₂ = 377 мм и толщиной стенки δ = 6 мм. Скорость стацио­нарного течения несжимаемой жидкости в первом участке составляет 1,2 м/с. Какова скорость течения жидкости во втором?

Ответ: 2,38 м/с

Примечание: Потерями на стыке участков пренебречь.

Дата добавления: 2015-10-29