Метод анализа размерностей, Пи-теорема

Анализ (или метод) размерностей используется во многих задачах физики и механики, а особенно в механике жидкости как для проверки ранее предложенных зависимостей, так и для составления новых. Анализ размерностей основан на так называемой ПИ-теореме, кото­рую можно сформулировать следующим образом: математическую зависимость между некоторыми физическими размерными величинами всегда можно преобразовать в уравнение, содержащие безразмерные комбинации тех же физических величин (так называемые числа ПИ), причем число этих безразмерных комбинаций всегда меньше, чем чис­ло исходных физических величин. Пусть A ₁, A ₂, A ₃,… A_n – n размерных физических величин, участвующих в каком-либо физическом явлении. Примером их могут служить скорость, вязкость, плотность и т. д. Пусть m – число всех первичных или основных единиц (например, длина, масса и время), с помощью которых можно представить размерность рассматриваемых физических величин. Функциональная зависимость между величинами A_i, может быть представлена в виде

f (A ₁, A ₂, A ₃,… A_n) = 0. (5.4)

Согласно ПИ-теореме это уравнение можно записать в виде

F (p₁, p₂, p₃,…p _n–m) = 0. (5.5)

где каждое число p – независимое безразмерное произведение несколь­ких А. Заметим, что число членов уравнения сократилось от п до п – т.

В задачах механики жидкости имеется три первичных размерности (масса, время, длина), т. е. m = 3. В этом случае максимальное число независимых комбинаций можно получить, выражая числа p в виде

(5.6)

В каждом числе p имеется m +1 переменное (и только одно переменное меняется от числа к числу) и три неизвестных показателя x, y и z. Рассматривая три первичные размерности, например L, T, M, получим три независимых уравнения, одновременное решение которых дает численное значение для трех показателей. Таким образом, для нахождения чисел ПИ нужно:

a) выбрать из числа переменных количество переменных, равное числу основных единиц и включающих все основные единицы;

б) составить уравнения размерностей, объединяющие выбранные переменные с каждой из других переменных по очереди.

Найдем, используя метод размерностей, общую формулу для определения потерь напора на трение при равномерном напорном движении жидкости в трубах.

Опыты показывают, что величина потерь напора на трение h _тр при движении жидкости в трубах может зависеть от диаметра трубы d и ее длины l, физических свойств жидкости (плотности r и вязкости m), средней скорости течения в трубе u, средней высоты выступов шероховатости k на стенках трубы. Таким образом, интересующую нас функциональную зависимость запишется в виде

D p _тр = f (u, d, m, r, k, l), (5.7)

где D p _тр – потери давления на длине потока, равной l, связанные с потерей напора формулой

D p _тр = g× h _тр. (5.8)

Вид функции f в уравнении (5.7) неизвестен. Некоторую помощь в установлении его может оказать применение ПИ-теоремы.

Учитывая, что потеря на трение всегда прямо пропорциональна длине рассматриваемого участка, перепишем уравнение (5.7) в виде

f ₁ (D p _тр/ l, u, d, m, r, k) = 0, (5.9)

Для измерения входящих в формулу (5.9) n = 6 величин требуется m = 3 основные единицы: масса, время и длина.

В соответствии с ПИ-теоремой уравнение (5.9) может быть представлено в форме, содержащей n – m = 3 безразмерных отношений (чисел ПИ), т. е. вместо (5.9) можно записать

f ₂ (p₁, p₂, p₃) = 0. (5.10)

Для определения чисел p₁, p₂, p₃ выберем из всех переменных три (по числу основных единиц измерения), включающие все основные единицы измерения, например u, d и r. Составим теперь уравнения размерностей, объединяющие выбранные переменные с каждой из других переменных по очереди, т. е

(5.11)

В выражениях для p₁, p₂, p₃ нужно подобрать показатели при d, u и r таким образом, чтобы числа p не имели размерности.

Так, например, для числа p₃ имеем

.

Отсюда вытекают следующие уравнения:

при L: x ₃ + y ₃ – 3 z ₃ + 1 = 0; при T: – y ₃ = 0; при M: z ₃ = 0, т.е. x₃ = –1 и

p₃ = k/d. (5.12)

Нетрудно показать (проверив размерности), что

p₁ = ud r/m. (5.13)

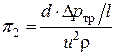. (5.14)

Подставляя (5.12), (5.13) и (5.14) в (5.10), имеем

Так как нас интересует потеря напора, то разрешаем это уравнение относительно p₂

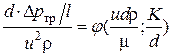или . (5.15)

Учитывая формулу (5.8), имеем

(5.16)

или, обозначая

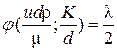, (5.17)

где l – безразмерное число, называемое коэффициентом гидравличес­кого трения, получим формулу Дарси – Вейсбаха

. (5.18)

Из формулы (5.18) следует, что потери напора на трение при движении жидкости в трубе возрастают с увеличением средней скорости потока и длины рассматриваемого участка трубы и обратно пропорциональны диаметру трубы.

Приведенный метод можно использовать и для определения вида формулы потерь напора на местные сопротивления. В этом случае, учитывая, что местные потери практически не зависят ни от длины участка трубы, ни от ее диаметра, нетрудно получить формулу

(5.19)

где x – безразмерный коэффициент, называемый коэффициентом мест­ных потерь; u ₂ – скорость после прохода через местное сопротивление.

Данная формула была получена в XIX в. эмпирическим путем и называется формулой Вейсбаха.

Таким образом, хотя с помощью ПИ-теоремы не удается получить полного решения вопроса о потерях напора (так как смысл коэффициентов l, x остался невыясненным), можно ближе подойти к его выяснению. Дальнейшие сведения о коэффициентах l, x будут рассмотрены в следующем пункте и §6.

Дата добавления: 2015-10-29