Дискретные случайные величины и их характеристики

Пусть имеется случайный эксперимент и задано вероятностное пространство .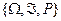

Случайной величиной 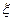называется функция , отображающая множество элементарных исходов на множество действительных чисел, и такая, что при любом множество тех исходов 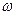, для которых 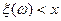, принадлежит 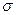-алгебре событий данного эксперимента.

Для тех, кто не собирается забивать голову понятиями, связанными с 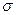-алгеброй событий, можно считать, что случайная величина есть любая функция из 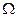в , то есть величина, принимающая в результате испытания то или иное числовое значение, в зависимости от исхода испытания.

Среди случайных величин можно выделить два основных типа: дискретные случайные величины и непрерывные случайные величины. Определим пока эти величины следующим образом:

Дискретной случайной величиной называется случайная величина, которая может принимать конечное или счетное множество значений.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями или множествами значений случайной величины и соответствующими им вероятностями.

Говорят, что случайная величина 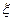имеет дискретное распределение, если она может принять конечное или счетное множество значений 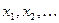с вероятностями 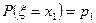, , 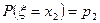, причем .

Рядом распределения дискретной случайной величины называется совокупность всех возможных значений случайной величины и соответствующих им вероятностей.

Обычно ряд распределения задают в виде таблицы:

ξ	х1	х2	…	хn
P	р1	р2	…	рn

либо аналитически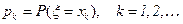

Графическое изображение ряда распределения называется многоугольником распределения. Для его построения возможные значения случайной величины 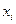откладываются по оси абсцисс, а вероятности - по оси ординат; точки c координатами 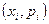соединяются ломаными линиями.

Ряд распределения можно составить только для дискретной случайной величины. Действительно, непрерывная случайная величина может принимать бесконечное множество значений, которые перечислить нельзя. Да и вероятность каждого отдельного значения этой случайной величины не может быть отличной от нуля. Поэтому, для характеристики распределения вероятностей таких величин используют не вероятности отдельных значений, а вероятности попадания этих значений в некоторый интервал.

Функцией распределения случайной величины 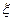называется функция , значение которой в каждой точке равно вероятности того, что случайная величина 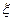примет значение меньшее 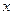, то есть:

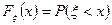. (1)

Свойства функции распределени:.

1) Функция распределения 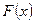есть неубывающая функция, то есть, если 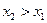, то .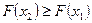

2) , .

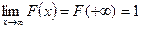3) Функция 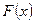непрерывна слева в каждой точке, т.е.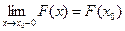

4) , или .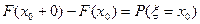

5) Если функция распределения непрерывна в точке 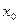, то .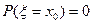

6) Вероятность попадания случайной величины на интервал 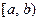равна разности значений функции распределения в граничных точках интервала:

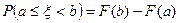
Значение функции распределения дискретной случайной величины для любого может быть найдено по формуле:

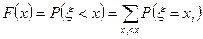, (2)

где суммирование идет по всем значениям случайной величины 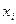меньшим величины .

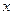Заметим, что для дискретной случайной величины, функция распределения представляет ступенчатую функцию, имеющую разрывы 1-го рода в точках, отвечающих возможным значениям случайной величины. Величина разрыва равна вероятности этих значений.

Упражнения:

1. Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте и построить многоугольник полученного распределения.

2. В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать закон распределения дискретной случайной величины X – числа нестандартных деталей среди четырёх отобранных и построить многоугольник полученного распределения.

3. Написать закон распределения случайной величины X – числа появлений «герба» при двух бросаниях монеты. Построить многоугольник полученного распределения.

4. Дискретная случайная величина X принимает три возможных значения: x ₁= - 4 с вероятностью p ₁=0,2; x ₂=6 с вероятностью p ₂=0,3; x ₃=10с вероятностью p ₃=0,5. Найти математическое ожидание данной случайной величины.

5. Дискретная случайная величина X принимает три возможных значения: x ₁=0,21 с вероятностью p ₁=0,1; x ₂=0,54 с вероятностью p ₂=0,5; x ₃=0,61с вероятностью p ₃=0,4. Найти математическое ожидание данной случайной величины.

6. Дискретная случайная величина X принимает три возможных значения: x ₁=4 с вероятностью p ₁=0,5; x ₂=6 с вероятностью p ₂=0,3и x ₃ с вероятностью p ₃. Найти x ₃ и p ₃, зная, что M (X)=8.

7. Найти дисперсию и среднее квадратичное отклонение дискретной величины X, заданной законом распределения:

X	-5
p	0,4	0,3	0,1	0,2

8. Найти дисперсию и среднее квадратичное отклонение дискретной величины X, заданной законом распределения:

а)

X	4,3	5,1	10,6
p	0,2	0,3	0,5

б)

X
p	0,05	0,10	0,25	0,60

9. Найти дисперсию дискретной случайной величины X – числа появлений события А в пяти независимых испытаниях, если вероятность появления события А в каждом испытании равна 0,2.

10. Найти дисперсию дискретной случайной величины X – числа отказав элемента некоторого устройства в десяти независимых опытах, если вероятность отказа элемента в каждом опыте равна 0,9.

11. Найти дисперсию дискретной случайной величины X – числа появлений события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что М (X)=1,2.

12. Дискретная случайная величина X имеет только два возможных значения x ₁ и x ₂, причём x ₂> x ₁. Вероятность того, что X примет значение x ₁, равна 0,6. Найти закон распределения величины X, если математическое ожидание и дисперсия известны: M (X)=1,4; D (X)=0,24.

13. Дискретная случайная величина X имеет только два возможных значения x ₁ и x ₂, причём x ₁< x ₂. Вероятность того, что X примет значение x ₁, равна 0,2. Найти закон распределения величины X, зная математическое ожидание M (X)=2,6 и среднее квадратичное отклонение σ(X)=0,8.

14. Дискретная случайная величина X имеет только три возможных значения x ₁=1, x ₂ и x ₃, причём x ₁< x ₂< x ₃. Вероятность того, что X примет значение x ₁ и x ₂ соответственно равны 0,3 и 0,2. Найти закон распределения величины X, зная математическое ожидание M (X)=2,2 и дисперсию D (X)=0,76.

Дата добавления: 2015-10-28