Формула полной вероятности, формула Байеса

Если при наступлении события 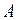вероятность события 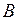не меняется, то события 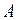и 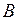называются независимыми.

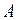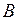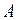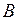Теорема: Вероятность совместного появления двух независимых событий и (произведения и ) равна произведению вероятностей этих событий.

События 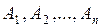называются попарно независимыми, если независимы любые два из них.

События 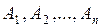называются независимыми в совокупности, если каждое из этих событий и событие равное произведению любого числа остальных событий, независимы.

Теорема: Вероятность произведения конечного числа независимых в совокупности событий 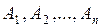равна произведению вероятностей этих событий.

.

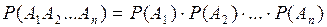Теорема (формула полной вероятности). Пусть события 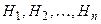образуют полную группу несовместных событий. Будем эти события называть гипотезами. Тогда вероятность любого события 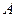того же поля событий равна:

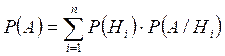
Теорема 2 (формула Байеса). Пусть событие 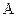, которое могло произойти вместе с одним из событий 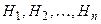, образующих полную группу несовместных событий, наступило. Тогда условная вероятность того, что осуществилась гипотеза 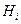равна:

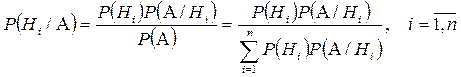
Поскольку данная формула позволяет вычислить апостериорные вероятности по априорным, то ее также называют формулой переоценки гипотез.

Упражнения:

1. В урну содержащую два шара, опущен белый шар, после чего из неё на удачу извлечён один шар. Найти вероятность того, что извлечённый шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).

2. В вычислительной лаборатории имеются шесть компьютеров модели А и четыре модели С.Вероятность того, что за время выполнения некоторого расчета компьютер модели А не выйдет из строя, равна 0,95; для компьютер модели С эта вероятность равна 0,8. Студент производит расчёт на наудачу выбранном компьютере. Найти вероятность того, что до окончания расчёта компьютер не выйдет из строя.

3. В сборочный цех поступили детали с трех станков. На первом станке изготовлено 51% деталей от их общего количества, на втором станке 24% и на третьем 25%. При этом на первом станке было изготовлено 90% деталей первого сорта, на втором 80% и на третьем 70%. Определить, какова вероятность того, что взятая наугад деталь окажется первого сорта?

4. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60 % деталей отличного качества, а второй – 84 %. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.

5. Число грузовых автомашин, проезжающих по шоссе. На котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.

6. Имеется три одинаковых по виду ящика. В первом ящике находится 26 белых шаров, во втором 15 белых и 11 черных, в третьем ящике 26 черных шаров. Из выбранного наугад ящика вынули белый шар. Вычислить вероятность того, что белый шар вынут из первого ящика.

7. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов?

8. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460—на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го — 0,02, для 3-го — 0,01. Взятый наудачу подшипник оказался нестандартным. Какова вероятность того, что он изготовлен 1-м заводом?

9. Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно рано 20, 15, 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию и вторично из той же партии наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали были извлечены из третьей партии.

10. Три стрелка производят по одному выстрелу в одну и ту же мишень. Вероятность попадания в мишень при одном выстреле для каждого из стрелков соответственно равны р ₁, р ₂, р ₃. Какова вероятность того, что второй стрелок промахнулся, если после выстрелов в мишени оказалось две пробоины?

11. имеется 12 урн, из них в 6 урнах (состав H ₁) по 3 белых и 4 чёрных шара, в 3 урнах (состав H ₂) по 2 белых и 8 чёрных шаров, в 2 урнах (состав H ₃) по 6 белых и 1 чёрному шару, в 1 урне (состав H ₄) 4 белых и 3 чёрных шара. Из наугад выбранной урны взят шар. Чему равна вероятность того, что шар взят из урны состава А ₃, если он оказался белым?

12. Батарея из трёх орудий произвела залп, причём два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны р₁=0,4, р₂=0,3, р₃=0,5.

Дата добавления: 2015-10-28