Повторение испытаний

Испытания называют независимыми относительно события А, если вероятность появления события А в каждом испытании не зависит от исходов других испытаний.

Рассмотрим независимые испытания, в которых вероятность появления события А постоянна и не меняется от опыта к опыту. При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент называется схемой повторных независимых испытаний или схемой Бернулли.

Пусть в результате n независимых испытаний, проведенных в одинаковых условиях, событие А наступает с вероятностью Р(А) = р, а противоположное ему событие 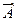с вероятностью .

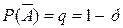Теорема (формула Бернулли):Если производится n независимых испытаний, в каждом из которых событие А появится с вероятностью р, то вероятность того, что событие А появится ровно k раз в n испытаниях, выражается формулой

P_n(k) = C_n^kp^k q^{n – k} (1)

Формула Бернулли описывает, как распределяются вероятности между возможным числом появления события A в n испытаниях.

Использование формулы Бернулли при больших значениях n затруднительно. В этом случае в теории вероятностей применяют асимптотические (предельные) формулы, которыми можно заменить формулу Бернулли, не вызывая этим заметных погрешностей в вычислениях.

Функция у(x) называется асимптотическим приближением функции f(x), если .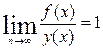

Часто интерес представляет случай большого числа n и малой вероятности p успеха в одном отдельном испытании. В этом случае удобно воспользоваться приближением Пуассона.

Теорема (Формула Пуассона): Если вероятность p наступления события А в каждом испытании постоянна и близка к нулю (р ), а число независимых испытаний n достаточно велико (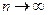), причем произведение np стремится к постоянному числу 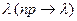то вероятность P_n(k) того, что в n независимых испытаниях событие А наступит k раз, приближенно равна:

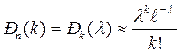(2)

Локальная теорема Муавра-Лапласа (рекомендуется применять при npq ).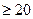

Пусть в серии из n независимых испытаний вероятность наступления события А в каждом испытании равна р (0<p<1), q=1-p,тогда вероятность Р_n(m) того, что событие А произойдет m раз в серии из n независимых испытаний при достаточно большом n, приближенно равна 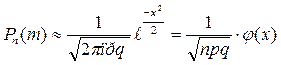(3),

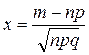где (4),

а функция 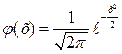(5) - функция Гаусса.

Для упрощения расчетов, связанных с применением функции 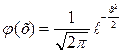, составлена таблица значений этой функции. Пользуясь таблицей, необходимо учитывать следующие свойства функции (5):

1. Функция 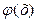является четной, т.е. = ;

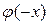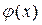2. Функция 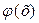является монотонно убывающей при х>0, причем уже при х>4 .

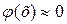Чем больше n, тем точнее приближенная формула (3). Приближенные значения, даваемые этой формулой на практике используются как точные при .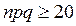

Интегральная теорема Муавра-Лапласа (удобно применять при npq ).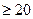

Пусть в серии из n независимых испытаний вероятность наступления события А в каждом испытании равна р (0<p<1), q=1-p,тогда вероятность Р_n(k₁,k₂) того, что событие А в серии из n независимых испытаний при достаточно большом n, произойдет в пределах от k₁ до k₂ раз включительно, приближенно равна

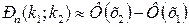(6),

где 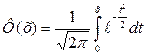- функция Лапласа (7),

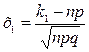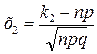, а (8).

Формула(6)называется интегральной теоремой Муавра-Лапласа.

Таблица значений функции 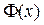приведена в приложении. Функция 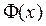является нечетной, т.е =- .

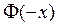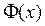Для упрощения расчетов, связанных с применением функции 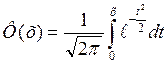, составлена таблица значений этой функции. Пользуясь таблицей, необходимо учитывать следующие свойства функции (7):

1. Функция 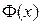является нечетной, т.е =- .

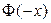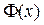2. Функция Ф(х) является монотонно возрастающей при х>0, причем уже при х>4 Ф(х) .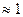

Чем больше n, тем точнее приближенная формула (6). Приближенные значения, даваемые этой формулой на практике используются как точные при .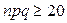

Упражнения:

1. Монету бросили 4 раза. Чему равна при этом вероятность выпадения герба два раза?

2. Вероятность изготовления нестандартной детали равна 0.11. Найти вероятность того, что из пяти наудачу взятых деталей будут четыре стандартных.

3. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырёх или три партии из шести (ничьи во внимание не принимаются)?

4. Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равно 0,25.

5. Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что событие появиться: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.

6. Найти вероятность того, что событие А наступит 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,6.

7. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.

8. Вероятность появления события в каждом из 21 независимых испытаний равна 0,7. Найти вероятность того, что событие появится в большинстве испытаний.

9. Вероятность выигрыша по облигации займа за всё время его действия равна 0,25. Какова вероятность того, что некто, приобретя 8 облигаций, выиграет по 6 из них?

10. Вероятность появления события в каждом из 2100 независимых испытаний равна 0,7. Найти вероятность того, что событие появится: а) не менее 1470 раз и не более 1500 раз; б) не менее 1470 раз; в) не более 1469 раз.

11. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорождённых окажется 50 мальчиков.

12. В урне 10 белых и 5 чёрных шаров. Используя формулу Бернулли найти вероятность того, что вынув наудачу с возвращением 14 шаров, получим белых не менее 12?

13. 30 % изделий данного предприятия – это продукция высшего сорта. Некто приобрёл 6 изделий, изготовленных на этом предприятии. Чему равна вероятность того, что 4 из них высшего сорта?

14. Вероятность появления события в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие появится не менее 75 раз?

---

Дата добавления: 2015-10-28