Статистические оценки параметров распределения

Пусть закон распределения генеральной совокупности определён с точностью до значений входящих в его распределение параметров 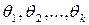, часть из которых может быть известна.

Оценка неизвестных параметров заключается в построении функции 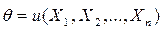от случайной выборки, такой, что значение этой функции приближённо равно оцениваемому неизвестному параметру θ. Функция 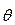называется статистикой параметра θ.

Статистической оценкой (в дальнейшем просто оценкой) 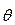параметра θ теоретического распределения называется его приближённое значение, зависящего от данных выбора.

Оценка 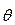является случайной величиной, т.к. является функцией независимых случайных величин 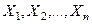; если произвести другую выборку, то функция примет, вообще говоря, другое значение.

Существует два вида оценок – точечные и интервальные.

Точечной называется оценка, определяемая одним числом. При малом числе наблюдений эти оценки могут приводить к грубым ошибкам. Чтобы избежать их, используют интервальные оценки.

Интервальной называется оценка, которая определяется двумя числами – концами интервала, в котором с заданной вероятностью заключена оцениваемая величина θ.

Величину 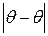называют точностью оценки. Чем меньше 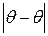, тем лучше, точнее определён неизвестный параметр.

Оценка 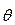параметра θ называется несмещённой (без систематических ошибок), если математическое ожидание оценки совпадает с истинным значением θ:

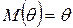. (1)

Если равенство (1) не имеет места, то оценка 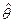называется смещённой (с систематическими ошибками).

Оценка 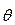называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещённых оценок параметра θ.

Пусть D (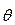) – минимальная дисперсия, а 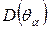– дисперсия любой другой несмещённой оценки 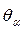параметра θ. Тогда эффективность оценки 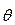равна

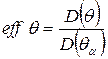. (2)

Ясно, что 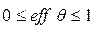. Чем ближе 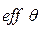к 1, тем эффективнее оценка 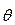. Есл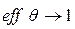и при 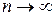, то оценка называется асимптотически эффективной.

Оценка 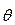называется состоятельной, если с увеличением объема выборки (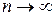) оценка сходится по вероятности к точному значению параметра θ, т.е. если для любого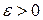

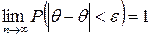. (3)

Состоятельность оценки 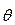параметра θ означает, что с ростом n объема выборки качество оценки 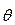улучшается.

Теорема 1. Выборочная средняя является несмещённой и состоятельной оценкой математического ожидания.

Теорема 2. Исправленная выборочная дисперсия является несмещённой и состоятельной оценкой дисперсии.

Теорема 3. Эмпирическая функция распределения выборки является несмещённой и состоятельной оценкой функции распределения случайной величины.

Универсального метода нахождения точечных оценок не существует. Имеется несколько хорошо зарекомендовавших себя методов нахождения этих оценок. Рассмотрим некоторые из них.

1. Метод моментов (Пирсона). Пусть известен закон распределения случайной величины X, содержащий неизвестные параметры 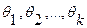. Произведём выборку объема n этой случайной величины. По методу моментов k выборочных моментов приравниваются к k первым моментам случайной величины X. Из полученной системы уравнений и находим оценки 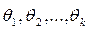параметров .

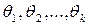Так, если распределение зависит от одного параметра θ (например, задан вид плотности распределения 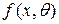), то для нахождения его оценки надо решить относительно θ одно уравнение:

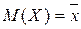. (4)

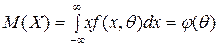( есть функция от θ).

Если распределение зависит от двух параметров (например, вид плотности распределения 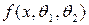), то надо решить относительно θ₁ и θ₂ систему уравнений:

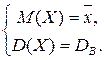(5)

И, наконец, если надо оценить n параметров 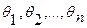- надо решить одну из систем вида:

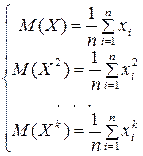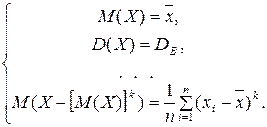или (6)

2. Метод максимального правдоподобия (МП-метод). Этот метод разработан английским математиком Р.Э. Фишером. Оценки, получаемые с его помощью, как правило, являются наиболее надёжными и особенно предпочтительны в случае малого числа наблюдений.

Метод максимального правдоподобия состоит в определении оценок 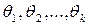, максимизирующих функцию правдоподобия 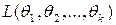. Эта функция строиться следующим образом. Пусть 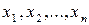- результаты наблюдений случайных величин 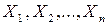, совместное распределение вероятностей которых зависит от неизвестных параметров 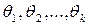, т.е. представляет собой условную плотность вероятностей 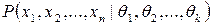. Условная плотность совместного распределения вероятностей случайных величин 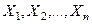называется функцией правдоподобия. При фиксированных значениях выборки 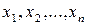функция правдоподобия является только функцией неизвестных параметров, т.е. .

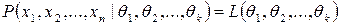По методу максимального правдоподобия в качестве оценок для 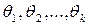выбираются такие значения 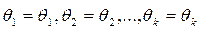, при которых «наблюдаемые» величины 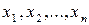наиболее вероятны, другими словами, значения 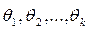максимизируют функцию правдоподобия .

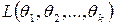Пусть X – дискретная случайная величина и 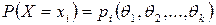, 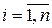- её закон распределения вероятностей. Тогда вероятность того, что элементы выборки (независимые случайные величины 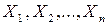) примут конкретные значения 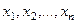, определяется равенством

.

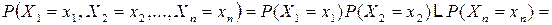
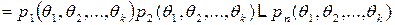Поскольку эта функция определяет совместное распределение вероятностей, то, следовательно, она является функцией правдоподобия. Таким образом, для дискретной случайной величины с законом распределения 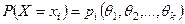функция правдоподобия определяется соотношением

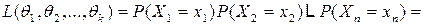
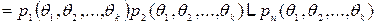. (7)

При оценке параметров распределения непрерывной случайной величины X с плотностью распределения 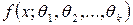по МП-методу функция правдоподобия определяется следующим образом:

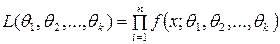, (8)

где 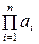- произведение .

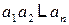Оценка параметров θ _i, построенная по выборочным значениям случайной величины X и максимизирующая функцию 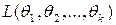, называется оценкой максимального правдоподобия или МП-оценкой.

Для упрощения вычислений МП-оценок часто бывает удобным рассматривать логарифм функции правдоподобия, т.е. .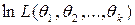

При максимизации функции (8) x _i считаются фиксированными, а МП-оценки параметров 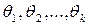определяются решением системы уравнений

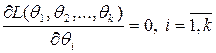, (9)

или

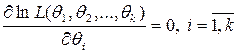. (10)

Системы (9) или (10) называются системами уравнений правдоподобия.

3. Метод наименьших квадратов. Пусть требуется измерить некоторую величину X и по результатам n измерений 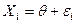, , 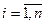где ε_i – ошибки измерений, а θ – точное значение измеряемой величины.

По методу наименьших квадратов требуется найти такое значение 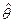, являющееся оценкой неизвестного параметра θ, которое минимизирует функцию

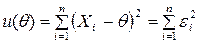, (11)

т.е. минимизирует сумму квадратов отклонений выборочных данных от параметра θ.

Упражнения:

1. Случайная величина X распределена по закону Пуассона 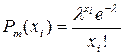в соответствии со следующей таблицей:

x i
n i

Найти методом моментов точечную оценку неизвестного параметра распределения Пуассона.

Указание: Учесть, что математическое ожидание распределения Пуассона равно параметру λ этого распределения.

2. Случайная величина X распределена по показательному закону 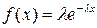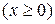в соответствии со следующей таблицей:

x i	2,5	7,5	12,5	17,5	22,5	27,5
n i

Найти методом моментов точечную оценку неизвестного параметра показательного распределения.

Указание: Учесть, что величина обратная математическому ожиданию показательного распределения равно параметру λ этого распределения.

3. Случайная величина X подчинена нормальному закону распределения 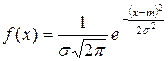в соответствии со следующей таблицей:

x i	0,3	0,5	0,7	0,9	1,1	1,3	1,5	1,7	1,9	2,2	2,3
n i

Найти методом моментов точечные оценки неизвестных параметров нормального распределения.

4. Случайная величина X распределена по равномерному закону 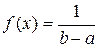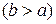в соответствии со следующей таблицей:

x i
n i

Найти методом моментов точечные оценки неизвестных параметров равномерного распределения.

Указание: Учесть, что для равномерного распределения , .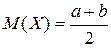

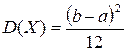5. Случайная величина X распределена по закону Пуассона в соответствии со следующей таблицей:

x i
n i

Найти методом моментов точечную оценку неизвестного параметра λ распределения Пуассона.

6. Найти доверительный интервал для оценки с надёжностью 0,95 неизвестного математического ожидания нормально распределённого признака X генеральной совокупности, если 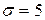, 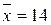и объем выборки n =25.

7. Найти минимальный объём выборки, при котором с надёжностью 0,975 точность оценки математического ожидания генеральной совокупности по выборочной средней равна 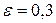, если известно среднее квадратичное отклонение 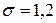нормально распределённой генеральной совокупности.

8. Из генеральной совокупности извлечена выборка объёма n =10:

x i	-2
n i

Оценить с надёжностью 0,95 математическое ожидание нормально распределённого признака генеральной совокупности по выборочной средней при помощи доверительного интервала.

9. Найти минимальный объём выборки, при котором с надёжностью 0,925 точность оценки математического ожидания нормально распределённой генеральной совокупности по выборочной средней равна 0,2, если известно среднее квадратичное отклонение генеральной совокупности .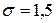

10. Из генеральной совокупности извлечена выборка объёма n =12:

x i	-0,5	-0,4	-0,2		0,2	0,6	0,8		1,2	1,5
n i

Оценить с надёжностью 0,95 математическое ожидание нормально распределённого признака генеральной совокупности с помощью доверительного интервала.

Дата добавления: 2015-10-28