
Если линии регрессий отличны от прямых, то коэффициент корреляции не даёт полного представления о силе связи между величинами X и Y. В этом случае за меру зависимости берут корреляционные отношения, которые вычисляют по формулам:
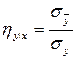 ,
, 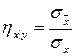 , (8)
, (8)
где
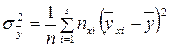 ;
; 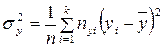 ;
;
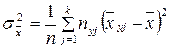 ;
; 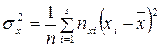 ;
;
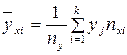 ;
; 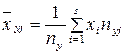 .
.
Корреляционное отношение обладает следующими свойствами:
1) оно всегда заключено между 0 и 1, т.е. 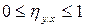 и
и 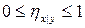 ;
;
2) необходимое и достаточное условие отсутствия корреляционной зависимости признака Y от признака X состоит в том, что 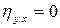 ;
;
3) если корреляционные отношения 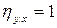 , то между признаком Y и признаком X существует функциональная зависимость
, то между признаком Y и признаком X существует функциональная зависимость 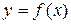 ;
;
4) выборочный коэффициент корреляции между признаками X и Y всегда по абсолютной величине не больше корреляционных отношений 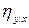 и
и 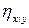 :
: 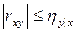 ,
, 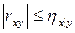 ;
;
5) если 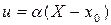 , а
, а 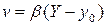
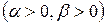 , то
, то 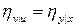 и
и 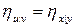 .
.
Для выбора и обоснования типа кривой регрессии нет универсального метода. Односторонняя зависимость между величинами X и Y может быть описана, например, с помощью полиномиальной регрессии:
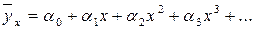
Упражнения:
1. По данным таблицы наблюдений
| xi | ||||
| yi |
составить уравнение регрессии Y на X (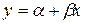 ) и X на Y (
) и X на Y (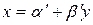 ).
).
2. По данным таблицы наблюдений
| Y | X | ||||
| - | |||||
| - | - |
составить уравнение регрессии Y на X (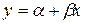 ).
).
3. По данным таблицы наблюдений
| xi | ||||
| yi |
составить уравнение регрессии 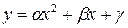 .
.
4. По данным таблицы наблюдений
| Y | X | ||
| - | - | ||
| - | |||
| - |
составить уравнение регрессии 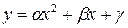 .
.
5. По данным таблицы наблюдений
| Y | X | ||
| - | - | ||
| - |
составить уравнение регрессии 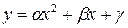 .
.
СПИСОК ЛИТЕРАТУРЫ
основная литература:
1. Вентцель, Е.С. Теория вероятностей [Текст] / Е.С. Вентцель. – М.: Высшая школа, 2006. – 575 с.
2. Вентцель, Е. С. Задачи и упражнения по теории вероятностей [Текст] / Е.С. Вентцель, Л. А.Овчаров - М.: Академия, 2005. - 448 с.
3. Гмурман, В.Е. Теория вероятностей и математическая статистика [Текст] / В.Е. Гмурман. - М.: Высшая школа, 2007. - 480 с.
дополнительная литература:
4. Вентцель, Е. С. Теория вероятностей и ее инженерные приложения [Текст]: учебное пособие / Е.С. Вентцель, Л. А.Овчаров - М.: Академия, 2003. – 464 с.
5. Кремер, Н.Ш. Теория вероятностей и математическая статистика [Текст] / Н.Ш. Кремер - М: ЮНИТИ, 2002. – 543 с.
6. Пентус, А.Е. Теория формальных языков [Текст] / А.Е. Пентус, М.Р. Пентус. - М. Изд-во МГУ, 2004. - 80 с.
Дата добавления: 2015-10-28; просмотров: 228 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Статистические оценки параметров распределения | | | Босс управляет, босс вдохновляет 4 страница |