Теоремы сложения и умножения вероятностей

Множество попарно несовместных событий называют полной группой событий, если при любом исходе случайного эксперимента непременно наступает одно из событий, входящих в это множество. Другими словами, для полной группы событий 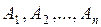выполнены следующие условия:

· появление одного из событий данного множества в результате испытания является достоверным событием, т.е. событие ;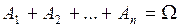

· события 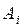и 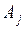(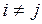) попарно несовместимы и
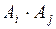– событие невозможное при любых 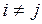, т.е. .

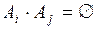Простейшим примером полной группы событий является пара противоположных событи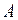й и .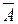

Теорема. Сумма вероятностей событий полной группы 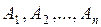равна единице:

.

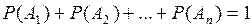Во многих случаях вероятности появления одних событий зависят от того, произошло другое событие или нет.

Вероятность события 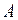, вычисленная при условии, что произошло другое событие 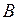, называется условной вероятностью события 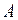и обозначается .

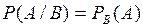Вероятность каждого события в данном испытании связана с наличием известного комплекса условий. При определении условной вероятности мы полагаем, что в этот комплекс условий обязательно входит событие 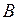. Таким образом, мы имеем другой, более обременительный комплекс условий, соответствующий испытанию в новой обстановке. Вероятность 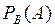появления события 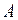при этих новых условиях называется его условной вероятностью в отличие от вероятности 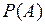, которая может быть названа безусловной вероятностью события .

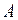В тех случаях, когда вероятность события 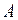рассматривается при условии, что имели место два других события 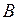и 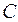, используется условная вероятность относительно произведения событий 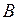и : .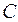

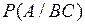Теорема: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:

.

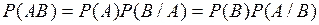Теорему умножения вероятностей легко обобщить на любое конечное число событий.

Теорема: Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих событий:

.

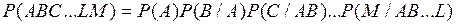Теорема: Вероятность суммы конечного числа несовместных событий 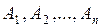равна сумме вероятностей этих событий:

.

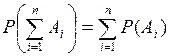Теорема: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

.

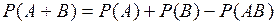Упражнения:

1. На стеллаже в случайном порядке расставлено 15 учебников, причём пять из них в переплёте. Студент берёт наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплёте (событие А).

2. В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.

3. Какова вероятность того, что при десятикратном бросании монеты герб выпадет 10 раз?

4. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания рабочего, для первого станка равна 0,9, для второго — 0,8, для третьего — 0,7. Найти: 1) вероятность р того, что в течение часа ни один из трех станков не потребует внимания рабочего; 2) вероятность того, что в течение часа по крайней мере один из станков не потребует внимания рабочего.

5. Вероятность появления каждого из двух независимых событий А ₁ и А ₂ соответственно равны р ₁ и р ₂. Найти вероятность появления только одного из этих событий.

6. Для сигнализации о пожаре установлены два независимо работающих сигнализатора. Вероятность того, что при пожаре сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при пожаре сработает только один сигнализатор.

7. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения в цель при одном выстреле первым из орудий, если известно, что для второго орудия вероятность попадания в цель при одном выстреле равна 0,8.

8. В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплёте. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплёте.

9. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу выбранные билета окажутся выигрышными.

10. В группе учатся семь мальчиков и три девочки. По номерам зачётных книжек наудачу отобраны три студента. Найти вероятность того, что все отобранные студенты оказались мальчиками.

11. В ящике 10 деталей, среди которых шесть окрашенных. Сборщик наудачу извлекает четыре детали. Найти вероятность того, что все извлечённые детали окажутся окрашенными.

12. В результате исследований было установлено, что темноглазые отцы и темноглазые сыновья (АВ) составили 5 % обследованных лиц, темноглазые отцы и светлоглазые сыновья (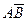) – 7,9 %, светлоглазые отцы и темноглазые сыновья (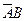) – 8,9 %, светлоглазые отцы и светлоглазые сыновья (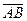) – 78,2 %. Найти связь между цветом глаз отца и сына.

13. Найти вероятность Р (А) по данным вероятностям: Р (АВ)=0,72; Р (А 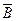)=0,18.

14. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадет только один из стрелков.

15. Один раз подбрасывается игральная кость. Событие А ={выпало простое число очков}, В={выпало чётное число очков}. Вычислить вероятность того, что выпавшее число простое при условии, что оно является чётным.

16. Вероятность попасть в самолёт равна 0,4, а вероятность его сбить равна 0,1. Найти вероятность того, что при попадании в самолёт он будет сбит.

17. Из колоды в 36 карт наудачу извлекается одна карта. События: А ={вынутая карта - туз}, B ={вынутая карта чёрной масти}, F ={вынутая карта - фигура, т.е. является валетом, дамой, королём или тузом}. Установить, зависимы или независимы следующие три пары событий: A и B, A и F, F и B.

18. Из 100 студентов, находящихся в аудитории, 50 человек знают английский, 40 – французский и 35 – немецкий. Английский и французский языки знают 20 студентов, английский и немецкий – 8, французский и немецкий – 10. Все три языка знают 5 человек. Один из студентов вышел из аудитории. Рассмотрим следующие события: E ={вышедший знает английский язык}, F ={ вышедший знает французский язык }, D ={ вышедший знает немецкий язык }.

а) Указать все пары независимых событий.

б) Установить, являются ли события E, F, D независимыми в совокупности.

19. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное.

20. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные экзаменатором три вопроса.

21. На складе находятся 26 деталей из которых 13 стандартные. Рабочий берет наугад две детали. Определить вероятность того, что обе детали окажутся стандартными.

22. В ящике лежат шары: 4 белых, 10 красных, 8 зеленых, 9 коричневых. Из ящика вынимают один шар. Определить, какова вероятность, что шар окажется цветным (не белым)?

Дата добавления: 2015-10-28