Вероятность события

Вероятность является количественной мерой возможности появления рассматриваемого события. Вероятность можно определить как функцию, заданную на подмножествах пространства .

Наиболее широкое распространение получило классическое определение вероятности события.

Классическое определение вероятности связано с определением благоприятствующего исхода. Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление этого события. Вероятность события 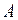равна отношению числа равновозможных благоприятствующих элементарных исходов к общему числу всех равновозможных и единственно возможных элементарных исходов данного испытания:

,

где – число благоприятствующих событию 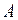исходов;

– общее число возможных исходов.

Из определения вероятности события 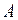следует, что 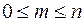, поэтому всегда выполняются неравенства , т.е. вероятность любого события есть неотрицательное число, не превышающее единицы.

Если 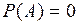, то событие 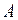невозможное.

Если 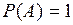, то событие 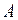достоверное.

Равновозможные элементарные события являются равновероятными, т.е. обладают одной и той же вероятностью.

Теорема. Эквивалентные события имеют одинаковые вероятности, т.е. если , то .

Теорема. Вероятность события , противоположного событию 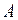равна дополнению вероятности данного события 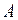до 1, т.е. .

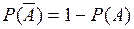Классическое определение вероятности предполагает, что:

· число элементарных исходов конечно;

· эти исходы равновозможны.

Упражнения:

1. Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях – четная, причем на грани хотя бы одной из костей появиться шестёрка.

2. При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь.

3. В магазин поступило 30 новых телевизоров, среди которых 5 имеют скрытые дефекты. Наудачу отбирается один телевизор для проверки. Какова вероятность, что он не имеет скрытых дефектов?

4. Автомат изготавливает однотипные детали, причем технология изготовления такова, что 5 % произведенной продукции оказывается бракованной. Из большой партии взята наудачу одна деталь для контроля. Найти вероятность события А={деталь бракованная}.

5. Игральная кость подбрасывается один раз. Найти вероятность следующих событий: A={число очков равно 6}, B={число очков кратно трём}, C={число очков чётно}, D={число очков меньше пяти}, Е={число очков больше двух}.

6. Подбрасываются две игральные кости. Найти вероятности следующих событий: A={числа очков на обеих костях совпадают}, B={число очков на первой кости больше, чем на второй}, C={сумма очков чётна}, D={сумма очков больше двух}, Е={сумма очков не меньше пяти}, F={хотя бы на одной кости появится цифра 6}, G={произведение выпавших очков равно 6}.

7. Наудачу выбирается пятизначное число. Какова вероятность следующих событий: A={число одинаково читается как слева направо, так и справа налево}, B={число кратно пяти}.

8. 1 сентября на третьем курсе одного из факультетов запланировано по расписанию три лекции по разным предметам. Всего на третьем курсе изучается 10 предметов. Студент, не успевший ознакомиться с расписанием, пытается его угадать. Какова вероятность успеха в данном эксперименте, если считать, что любое расписание их трёх предметов равновозможно?

9. Задумано двузначное число. Найти вероятность того, что задуманным числом окажется: а) случайно названное двузначное число; б) случайно названное двузначное число, цифры которого различны.

10. Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) сумма выпавших очков равна восьми, а разность – четырём; в) сумма выпавших очков равна восьми, если известно, что их разность равна четырём; г) сумма выпавших очков равна пяти, а произведение – четырём.

11. Монета брошена два раза. Найти вероятность того, что хотя бы один раз появиться «герб».

12. На коробке шесть одинаковых, занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлечённых кубиков появятся в возрастающем порядке.

13. Найти вероятность того, что при бросании трёх игральных костей шестёрка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (и не равные шести).

14. В ящике 10 одинаковых деталей, помеченных номерами 1, 2, …, 10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлечённых деталей окажутся: а) деталь № 1; б) детали № 1 и № 2.

15. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлечённые детали окажутся окрашенными.

16. В партии из 23 деталей находятся 10 бракованных. Вынимают из партии наудачу две детали. Определить, какова вероятность того, что обе детали окажутся бракованными.

Дата добавления: 2015-10-28