Комбинаторика

Комбинаторика - область математики, изучающая комбинации и перестановки различных объектов.

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения.

Правило суммы: пусть имеется n попарно непересекающихся множеств A₁, A₂, …, A_n, содержащих m₁, m₂, …, m_n элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно m₁ + m₂ + … + m_n.

Кортеж - конечная последовательность (допускающая повторения) элементов какого-нибудь множества.

Правило произведения (Основной принцип комбинаторики): пусть имеется n множеств A₁, A₂, …, A_n содержащих m₁, m₂, …, m_n элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества, т.е. построить кортеж (а₁,а₂,...,а_n), где а_iÎА_i1 (i = 1, 2, …, n), равно m₁·m₂·…·m_n.

основными задачами комбинаторики являются следующие:

1) образование упорядоченных подмножеств - составление размещений;2) образование упорядоченных множеств, состоящее в установлении определенного порядка следования элементов множества друг за другом, - составление перестановок;3) образование подмножеств, состоящее в выделении из данного множества некоторой части его элементов, - составление сочетаний.

Размещениями из n элементов по m элементов (m < n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов. Обозначаются .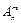

Размещения без повторений: Число размещений из n различных элементов по m элементов вычисляется по формуле:

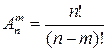(1).

Размещения с повторениями (n различных элементов, элементы могут повторяться):

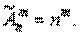(2)

Перестановками из n элементов называются размещения из этих n элементов по n, различающихся только порядком. Перестановки - частный случай размещений. Обозначаются .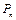

Перестановки без повторений (n различных элементов):

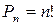(3).

Перестановки c повторениями (k различных элементов, где элементы могут повторяться m₁, m₂, …, m_k раз и m₁ + m₂ + … + m_k = n, где n - общее количество элементов):

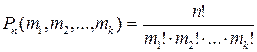(4).

Сочетаниями из n элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом. Обозначаются .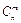

Отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов.

Сочетания без повторений (n различных элементов, взятых по m):

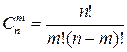(5).

Сочетания c повторениями (n элементов, взятых по m, где элементы в наборе могут повторяться):

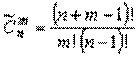(6).

Упражнения:

1. В вузовской столовой на первое можно заказать борщ, солянку, грибной суп, на второе - мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье - чай или компот. Сколько различных обедов можно составить из указанных блюд?

2. Свете на день рождения подарили 4 плюшевых игрушки, 2 мяча и 5 кукол. Мама положила все игрушки в большую коробку. Сколькими способами Света сможет достать из коробки 1 плюшевую игрушку, 1 мяч и 1 куклу?

3. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9?

4. Саша, Леня, Артем, Оля, Женя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения?

5. Из учащихся пяти 11 классов нужно выбрать двоих дежурных. Сколько пар дежурных можно составить (ученики в паре не должны быть из одного класса)?

6. Сколько перестановок можно сделать из букв слова «Миссисипи».

7. Мисс Марпл, расследуя убийство, заметила отъезжающее от дома мистера Дэвидсона такси. Она запомнила первую цифру “2”. В городке номера машин были трехзначные и состояли из цифр 1,2,3,4 и 5. Скольких водителей, в худшем случае, ей придется опросить, чтобы найти настоящего убийцу?

8. На втором курсе лучше всех математику знают 5 студентов: Вася, Дима, Олег, Катя и Аня. На олимпиаду по математике нужно отправить пару, состоящую из 1 мальчика и 1 девочки. Сколькими способами преподаватель может эту пару выбрать?

9. В соревнованиях по фигурному катанию принимали участие россияне, итальянцы, украинцы, немцы, китайцы и французы. Сколькими способами могут распределится места по окончании соревнований?

10. На втором курсе 6 человек (Галя, Света, Катя, Оля, Максим, Витя) учатся на все пятерки. Деканат премировал лучших студентов путевками в Анапу. Но, к сожалению, путевок всего четыре. Сколько возможно вариантов выбора студентов на отдых?

11. Пете на день рождения подарили 7 новых дисков с играми, а Вале папа привез 9 дисков из командировки. Сколькими способами они могут обменять 4 любых диска одного на 4 диска другого?

12. Войсковое подразделение состоит из 5 офицеров, 8 сержантов и 70 рядовых. Сколькими способами можно выделить отряд из 2 офицеров, 4 сержантов и 15 рядовых?

13. На выборах победили 9 человек - Сафонов, Николаев, Петров, Кулаков, Мишин, Гусев, Володин, Афонин, Титов. Из них нужно выбрать председателя, заместителя и профорга. Сколькими способами это можно сделать?

14. В ювелирную мастерскую привезли 6 изумрудов, 9 алмазов и 7 сапфиров. Ювелиру заказали браслет, в котором 3 изумруда, 5 алмазов и 2 сапфиров. Сколькими способами он может выбрать камни на браслет?

15. В студенческом общежитии в одной комнате живут трое студентов Петя, Вася и Коля. У них есть 6 чашек, 8 блюдец и 10 чайных ложек (все принадлежности отличаются друг от друга). Сколькими способами ребята могут накрыть стол для чаепития (так, что каждый получит чашку, блюдце и ложку)?

16. В районе построили новую школу. Из пришедших 25 человек нужно выбрать директора школы, завуча начальной школы, завуча среднего звена и завуча по воспитательной работе. Сколькими способами это можно сделать?

17. В кабинете заведующего ювелирного магазина имеется код, состоящий из двух различных гласных букв русского алфавита, за которой следуют 3 различные цифры. Сколько вариантов придется перебрать мошеннику, чтобы раздобыть драгоценности, которые там хранятся?

18. Сколькими способами можно составить трехцветный флаг из полос разной ширины, если имеются материи из 8 тканей?

19. На втором курсе 15 предметов. Деканату нужно составить расписание на субботу, если в этот день 5 пар занятий. Сколько различных вариантов расписания можно составить, если все занятия различны?

20. В огороде у бабушки растут 3 белые, 2 алые и 4 чайных розы. Сколькими различными способами можно составить букет из трех роз разного цвета?

21. Имеется пять различных стульев и семь рулонов обивочной ткани различных цветов. Сколькими способами можно осуществить обивку стульев.

22. Сколько может быть случая выбора 2 карандашей и 3 ручек из пяти различных карандашей и шести различных ручек?

23. На ферме есть 20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью? Если такой выбор уже сделан, сколькими способами можно сделать его еще раз?24. Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»?25. Сколько существует четных пятизначных чисел, начинающихся нечетной цифрой?

Дата добавления: 2015-10-28