Числовые характеристики выборки

Пусть x ₁, x ₂, …, x _n – выборка из генеральной совокупности объёма n.

Выборочной средней (или средним значение выборки) называется среднее арифметическое значение признака выборочной совокупности.

Если все значения x ₁, x ₂, …, x _n признака выборки объема n различны, то

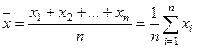. (1)

Если все значения признака x ₁, x ₂, …, x _k имеют соответственно частоты n ₁, n ₂, …, n _k, причем n ₁+ n ₂+ …+ n _k= n, то

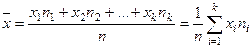. (2)

Если дано распределение непрерывной случайной величины, то вместо x _i, берут середину интервала, т.е. .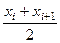

Выборочной дисперсией называется среднее арифметическое квадратов отклонения наблюдаемых значений выборки от их среднего значения .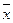

Если все значения x ₁, x ₂, …, x _n признака выборки объема n различны, то

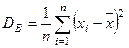. (3)

Если все значения признака x ₁, x ₂, …, x _k имеют соответственно частоты n ₁, n ₂, …, n _k, причем n ₁+ n ₂+ …+ n _k= n, то

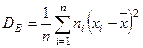. (4)

Для вычисления выборочной дисперсии можно пользоваться формулой:

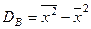. (5)

Выборочная дисперсия имеет систематическую ошибку, приводящую к уменьшению дисперсии. Чтобы это устранить вводят поправку, умножая D_B на 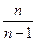. В результате получают исправленную (или модифицированную) дисперсию:

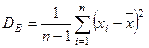. (6)

Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратичным отклонением.

Выборочным средним квадратичным отклонением (стандартом) называют квадратный корень из выборочной дисперсии:

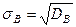. (7)

Средней гармонической выборки называется величина обратная средней арифметической из обратных значений вариантов:

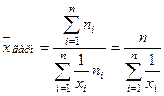. (8)

В некоторых исследованиях требуется определить среднюю величину так, чтобы при замене ею каждого варианта, произведение вариантов оставалось бы неизменным. Для этих целей используется средняя геометрическая.

Средней геометрической называется корень степени, равный числу вариантов, из их произведения:

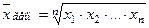. (9)

Средняя геометрическая применяется для характеристики средних темпов изменения какого-либо явления за определённый период (ежегодный рост числа читателей, среднегодовой прирост объема фонда и т.п.).

Отклонение каждого варианта от выборочного среднего 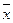характеризуется абсолютной величиной разности 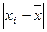, а весь ряд отклонений характеризует вариацию признака в совокупности.

Средним линейным отклонением называется средняя арифметическая абсолютных величин отклонений вариантов от их выборочной средней:

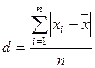. (10)

Кроме рассмотренных средних, в качестве общих характеристик признака могут быть использованы величины конкретных вариантов, занимающих в ранжированном ряду индивидуальных значений признака определённое положение. Особенно часто прибегают для общей характеристики признака к двум таким вариантам: моде и медиане.

Медианой М_е называется вариант, стоящий в центре ранжированного ряда, так что число вариант совокупности с большим и меньшим, чем медиана, значением признака одинаково.

Пусть имеется дискретный вариационный ряд. Если всем вариантам ряда придать порядковые номера, то номер медианы в ряду с нечётным числом членов n определится как 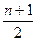. Если же вариантов чётное число, то медиану приходится определить как среднюю из двух центральных вариантов, порядковые номера которых 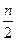и .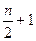

Однако если объем выборки достаточно большой и различия между вариантами небольшие, то можно считать медианой (с достаточной степенью точности) один из центральных вариантов с порядковым номером .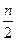

Для интервального распределения сначала находят медианный интервал 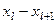(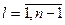). Номер его будет соответствовать интервалу, кумулятивная частота которого равна или превышает половину суммы частот:

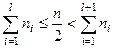. (11)

В случае выполнения равенства, стоящего в левой части формулы (11) номер медианного интервала равен l, в противном случае – l +1. Медиану вычисляют по формуле:

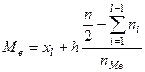, (12)

где l – порядковый номер интервала, где находится медиана, h – величина медианного интервала, 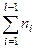- накопленная частота домедианного интервала, 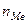- частота медианного интервала.

Модой М_о называется наиболее часто встречающаяся в совокупности величина варианта.

Для дискретного ряда мода определяется как значение признака с наибольшей частотой. В случае непрерывной вариации определяют модальный интервал 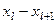, т.е. интервал, которому соответствует наибольшая частота 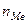. Мода вычисляется по формуле:

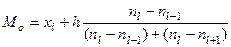, (13)

где n_{l -1} и n_{l +1} – частоты, которые находят в соответствии с предмодальным и послемодальным интервалами.

Для сравнения меры рассеяния значений признаков около выборочной средней в разных выборках служит коэффициент вариации. Наиболее распространены следующие коэффициенты:

- коэффициент вариации по среднему линейному отклонению

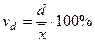, (14)

- коэффициент вариации по среднему квадратичному отклонению

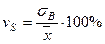. (15)

Особо часто употребляется последний коэффициент, и поэтому именно его иногда называют коэффициентом вариации без добавления показателя.

Таким образом, будем считать, что к оэффициентом вариации v называется отношение выборочного среднего квадратичного отклонения к выборочной средней, выраженное в процентах:

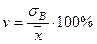. (16)

Простейшей мерой рассеяния случайной величины является размах выборки.

Размах выборки R это разность между наибольшим и наименьшим значениями выборки:

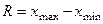. (17)

Выражения

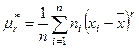, (18)

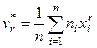, (19)

называются r -тым центральным и начальным моментами соответственно. Заметим, что , .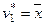

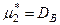Асимметрией выборки называется число

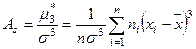. (20)

Эксцессом выборки называется число

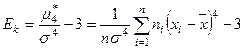. (21)

Упражнения:

1. Найти средние характеристики (выборочное среднее, выборочную дисперсию, выборочное среднее квадратичное отклонение, среднюю гармоническую, среднюю геометрическую, среднее линейное отклонение) для следующего дискретного вариационного ряда:

xi
ni

2. Найти средние характеристики (выборочное среднее, выборочную дисперсию, выборочное среднее квадратичное отклонение, среднюю гармоническую, среднюю геометрическую, среднее линейное отклонение) для следующего интервального вариационного ряда:

xi - xi+1	9-12	12-15	15-18	18-21	21-24	24-27
ni

3. Найти медиану следующего вариационного ряда: 3, 6, 6, 8, 8, 12, 12, 12, 25, 25, 70, 75, 75.

4. Найти моду и медиану интервального вариационного ряда, заданного таблицей:

x i - x i+1	n i
120-140
140-160
160-180
180-200
200-220
220-240
240-260
260-280

5. Найти медиану и моду дискретного вариационного ряда объема n =100, заданного таблицей:

x i	n i	n i нак
выше 6

6. Найти медиану и моду для интервального вариационного ряда, заданного таблицей:

x i - x i+1	n i
80-90
90-100
100-110
110-120
120-130
130-140
140-150

7. Найти асимметрию и эксцесс распределения, заданного таблицей:

x i	-2	-1
n i

8. Найти ковариацию 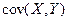по данным таблицы:

i
x i	-1
y i

9. Найти моду и медиану для интервального вариационного ряда, заданного таблицей:

x i - x i+1	n i
143-146
146-149
149-152
152-155
155-158
158-161
161-164
164-167
167-170
170-173
173-176
176-179
179-182
182-185
185-188

10. Найти медиану и моду для дискретного вариационного ряда, заданного таблицей:

x i
n i

11. Найти асимметрию и эксцесс распределения, заданного таблицей:

x i
n i

12. Найти медиану и моду для интервального вариационного ряда, заданного таблицей:

x i - x i+1	n i
70-80
80-90
90-100
100-110
110-120
120-130
130-140
140-150

Дата добавления: 2015-10-28