
|
Читайте также: |
Кемеровский государственный университет культуры и искусств
Институт информационных и библиотечных технологий
Кафедра технологии автоматизированной обработки информации
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Сборник задач
Направление подготовки:
230700 Прикладная информатика
Профиль подготовки:
Информационная сфера
Квалификация (степень) выпускника:
Бакалавр
Форма обучения:
очная, заочная
Кемерово 2014
Теория вероятностей и математическая статистика: Сборник задач по направлению подготовки 230700 «Прикладная информатика», профилю подготовки «Информационная сфера», квалификация (степень) выпускника – «бакалавр» /Сост. Э.Н. Огнева. – Кемерово: Кемеровский государственный университет культуры и искусств, 2014. - 89с.
Составитель:
доцент Огнева Э.Н.
СОДЕРЖАНИЕ
Введение......................................................... 3
Раздел 1 СЛУЧАЙНЫЕ СОБЫТИЯ...................................5
1.1. Алгебра событий.........................................5
1.2. Вероятность события..................................... 9
1.3. Комбинаторика......................................... 12
1.4. Теоремы сложения и умножения вероятностей...............17
1.5. Формула полной вероятности, формула Байеса...............22
1.6. Повторение испытаний...................................26
Раздел 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ................................31
2.1. Дискретные случайные величины и их характеристики........ 31
2.2. Предельные теоремы и закон больших чисел.................36
2.3. Непрерывные случайные величины и их характеристики.......42
2.4. Некоторые законы распределения случайных величин........ 47
Раздел 2. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ........... 55
2.1. Выборочный метод.......................................55
2.2. Числовые характеристики выборки......................... 67
2.3. Статистические оценки параметров распределения............76
2.4. Элементы теории корреляции..............................84
Список литературы................................................89
Введение
Дисциплина «Теория вероятностей и математическая статистика» входит в базовую часть цикла математических и естественнонаучных дисциплин образовательной программы по специальности 080801 «Прикладная информатика (в информационной сфере)». Для освоения дисциплины необходимы знания, умения и навыки, сформированные в результате изучения студентами дисциплин «Математика» и «Математическая логика».
Дисциплина «Теория вероятностей и математическая статистика» является предшествующей для дисциплин «Моделирование информационных ресурсов», «Системы принятия решений», «Методы анализа предметных областей», «Проектирование информационных систем».
Цель преподавания дисциплины «Теория вероятностей и математическая статистика» состоит в том, чтобы ознакомить студентов с элементами вероятностного и статистического аппарата, необходимого для решения прикладных задач; сформировать практические навыки по использованию законов распределения случайных величин в практических задачах, оцениванию генеральной совокупности и её параметров по данным выборочной совокупности.
Задачей дисциплины является формирование представлений о базовых понятиях, используемых для описания методов количественной оценки случайных событий и величин, а также знакомство студентов с основными методами теории вероятности и математической статистики. В соответствии с поставленными задачами в структуре дисциплины выделено три раздела. Первый раздел посвящен случайным событиям, во втором рассматриваются случайные величины; в третьем разделе изучаются элементы математической статистики.
В соответствии с учебным планом в составе общего объема часов, отводимых на изучения курса, предусмотрено 72 часа аудиторной и 62 часа самостоятельной работы. Занятия предусматривают чтение лекций и проведение практических занятий. В результате изучения дисциплины студент должен знать классификацию случайных событий и случайных величин, законы распределения случайных величин, закон больших чисел, методы статистического анализа; уметь вычислять вероятности случайных событий, составлять и исследовать функции распределения случайных величин, определять числовые характеристики случайных величин, обрабатывать статистическую информацию для оценки значений параметров и проверки значимости гипотез; владеть комбинаторным, теоретико-множественным и вероятностным подходами к постановке и решению задач, навыками статистической обработки эмпирических данных.
Настоящий сборник задачпредназначен для организации практических занятий и самостоятельной работы студентов. В составе сборника выделено 3 раздела, которые подразделяются на параграфы. Каждый параграф построен по унифицированной схеме, предусматривающей изложение определений важнейших терминов, основных теоремы и формулы, а также других кратких теоретических сведений, необходимых для решения предусмотренных учебной программой задач. Сборник содержит список литературы, который поможет студентам в подборе документов для получения дополнительных сведений по представленным темам и расширению круга заданий для самостоятельной работы.
Раздел 1. СЛУЧАЙНЫЕ СОБЫТИЯ
Алгебра событий
Случайное событие – это событие, которое может произойти, а может и не произойти. Наступление случайного события, независимо от его природы, характеризуется вероятностью или плотностью вероятности. Вероятность случайного события характеризует частоту наступления случайного события, если указанные события повторяются большое количество раз.
Каждый из равновозможных результатов испытаний называется элементарным исходом или (элементарным событием). Всякий мыслимый результат эксперимента называют элементарным событием и обычно обозначают буквами 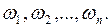
Пространством элементарных событий называется множество всех взаимно исключающих исходов эксперимента такое, что результатом эксперимента всегда является один и только один исход.
Пространство элементарных событий обычно обозначается  и считается заданным, если указаны все его элементы.
и считается заданным, если указаны все его элементы.
Два события называются совместными (совместимыми) в данном опыте, если появление одного из них не исключает появления другого.
Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий 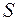 .
.
Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий 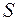 .
.
По аналогии с теорией множеств, строится алгебра событий. В частности, определены следующие операции и отношения между событиями:
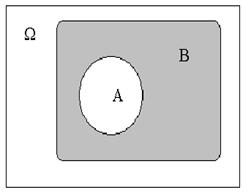
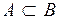
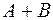
| 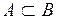 (отношение включения множеств: множество (отношение включения множеств: множество 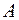 является подмножеством множества является подмножеством множества 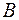 ) –событие A влечет за собой событие В. Иначе говоря, событие В происходит всякий раз, как происходит событие A. ) –событие A влечет за собой событие В. Иначе говоря, событие В происходит всякий раз, как происходит событие A.
 (отношение эквивалентности множеств) – событие (отношение эквивалентности множеств) – событие 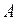 тождественно или эквивалентно событию тождественно или эквивалентно событию 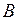 . Это возможно в том и только в том случае, когда . Это возможно в том и только в том случае, когда 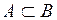 и одновременно и одновременно 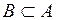 , т.е. каждое из них происходит всякий раз, когда происходит другое. , т.е. каждое из них происходит всякий раз, когда происходит другое.
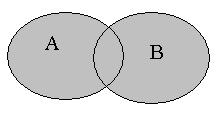
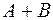 ( (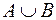 ) –сумма событий. Это событие, состоящее в том, что произошло хотя бы одно из двух событий ) –сумма событий. Это событие, состоящее в том, что произошло хотя бы одно из двух событий 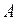 или или 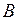 (не исключающее логическое «или»). В общем случае, под суммой нескольких событий понимается событие, состоящее в появлении хотя бы одного из этих событий. (не исключающее логическое «или»). В общем случае, под суммой нескольких событий понимается событие, состоящее в появлении хотя бы одного из этих событий.
| |
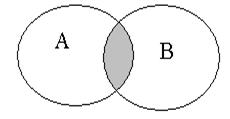
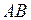
| 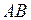 ( (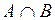 ) –произведение событий. Это событие, состоящее в совместном осуществлении событий ) –произведение событий. Это событие, состоящее в совместном осуществлении событий 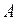 и и 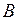 (логическое «и»). В общем случае, под произведением нескольких событий понимается событие, состоящее в одновременном осуществлении всех этих событий. Таким образом, события (логическое «и»). В общем случае, под произведением нескольких событий понимается событие, состоящее в одновременном осуществлении всех этих событий. Таким образом, события 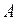 и и 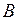 несовместны, если произведение их есть событие невозможное, т.е. несовместны, если произведение их есть событие невозможное, т.е. 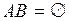 . .
| |
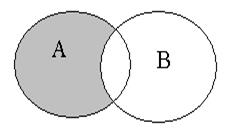
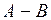
| 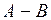 (множество элементов, принадлежащих (множество элементов, принадлежащих 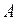 , но не принадлежащих , но не принадлежащих 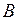 ) – разность событий. Это событие, состоящее из исходов, входящих в ) – разность событий. Это событие, состоящее из исходов, входящих в 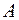 , но не входящих в , но не входящих в 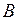 . Оно заключается в том, что происходит событие . Оно заключается в том, что происходит событие 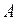 , но при этом не происходит событие , но при этом не происходит событие 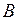 . .
| |
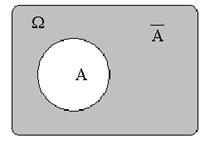
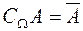
| Противоположным (дополнительным) для события 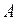 (обозначается (обозначается 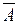 ) называется событие, состоящее из всех исходов, которые не входят в ) называется событие, состоящее из всех исходов, которые не входят в 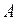 .
Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Событие .
Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Событие 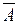 , противоположное событию , противоположное событию 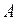 , происходит тогда и только тогда, когда событие , происходит тогда и только тогда, когда событие 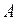 не происходит. не происходит.
| |
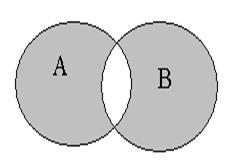
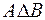
| Симметрическая разность двух событий 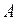 и и 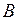 (обозн. (обозн. 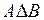 ) называется событие, состоящее из исходов, входящих в ) называется событие, состоящее из исходов, входящих в 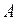 или или 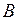 , но не входящих в , но не входящих в 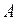 и в и в 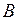 одновременно. Смысл события одновременно. Смысл события 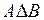 состоит в том, что наступает одно и только одно из событий состоит в том, что наступает одно и только одно из событий 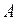 или или 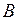 . . 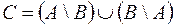 . Обозначается симметрическая разность: . Обозначается симметрическая разность: 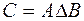 или или 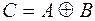 . .
| |
Упражнения:
1. Эксперимент состоит в подбрасывании один раз правильной шестигранной кости. Обозначим X число очков, выпавших на верхней грани очков. Описать множество элементарных исходов Ω и указать состав подмножеств, соответствующих следующим событиям: А ={X кратно трём}, B={X нечётно}, C={X>3}, D={X<7}, E={X дробно}, F={0,5<X<1,5}. Выявить пары совместных событий.
2. Эксперимент состоит в радиолокационном обнаружении воздушной цели. Наблюдаемый результат – положение светящегося пятна на экране, имеющего форму круга радиуса 10 см в декартовой системе координат с началом, совпадающим с центром экрана. Описать множество элементарных исходов и состав подмножеств, соответствующих следующим событиям: A={цель находится в первом квадранте}, B={цель находится в круге радиуса 5 см, центр которого совпадает с центром экрана}, C={ цель находится в круге радиуса 2,5 см, центр которого сдвинут на 5 см вдоль оси Ox в отрицательном направлении}. Совместны ли пары событий А и В, А и С, В и С.
3. Игральная кость подбрасывается дважды. Наблюдаемый результат – пара чисел, соответствующих числам очков, выпавших в первый и второй раз. Описать множество элементарных исходов Ω и состав подмножеств, соответствующих следующим событиям: A={оба раза выпало число очков, кратное трём}, B={ни разу не выпало число шесть}, C={оба раза выпало число очков, больше трёх}, D={Оба раза выпало одинаковое число очков}.
4. Монета подбрасывается три раза. Наблюдаемый результат – появление герба (Г) или цифры (Ц) на верхней стороне монеты. Описать множество элементарных исходов Ω и состав подмножеств, соответствующих следующим событиям: A={герб выпал ровно один раз}, B={ни разу не выпала цифра}, C={выпало больше гербов, чем цифр}, D={герб выпал не менее, чем два раза подряд}.
5. Игральная кость подбрасывается один раз. Наблюдаемый результат – число очков на верхней грани. События A, B, C, D, E, F описаны в примере 1. Описать состав и выяснить смысл следующих событий: 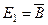 ,
, 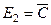 ,
, 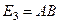 ,
, 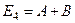 ,
, 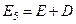 .
.
6. В отделе технического контроля проверяют очередную партию изделий. Взятая наудачу деталь может оказаться либо I сорта (событие А), либо II сорта (событие В), либо III сорта (событие С). Что представляют собой следующие события: 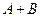 ,
, 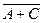 ,
, 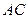 ,
, 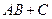 ?
?
Дата добавления: 2015-10-28; просмотров: 149 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Убеждайтесь в прохождении регистрации | | | Вероятность события |