Предельные теоремы и закон больших чисел

Свойство устойчивости массовых, случайных явлений известно человечеству еще с глубоких времен. В какой бы области оно не проявлялось, суть его сводится к следующему: конкретные особенности каждого отдельного случайного явления почти не сказывается на среднем результате массы таких явлений. Именно эта устойчивость средних и представляет собой физическое содержание " закона больших чисел ",понимаемого в широком смысле слова: при очень большом числе случайных явлений средний их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности.

Различные формы закона больших чисел вместе с различными формами центральной предельной теоремы образуют совокупность так называемых предельных теорем теории вероятности.

Предельные теоремы дают возможность не только осуществить научные прогнозы в области случайных явлений, но и оценивать точность этих прогнозов.

Неравенство Чебышева

Имеется случайная величина (СВ) 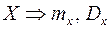. Неравенство Чебышева утверждает, что каково бы ни было положительное число 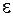, вероятность того, что СВ 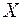отклонится от своего математического ожидания не меньше, чем на 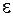, ограничена сверху величиной 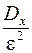, т.е.

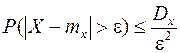. (1)

Неравенство Чебышева дает грубую оценку сверху и утверждает, что для любой случайной величины Х вероятность того, что она отклонится на 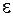от 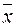меньше, чем дисперсия деленная на .

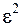Теорема Чебышева

Пусть имеется СВ 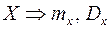. Над этой величиной производится 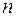независимых опытов и вычисляется среднее арифметическое всех наблюденных значений случайной величины Х. Необходимо найти характеристики среднего арифметического – математическое ожидание и дисперсию. В результате первого опыта СВ 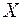приняла значение 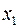, во втором опыте – 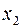,..., в 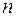– ом опыте – .

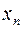Рассмотрим среднее арифметическое этих значений:

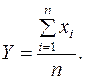(2)

СВ 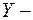линейная функция независимых случайных величин 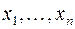. Определим:

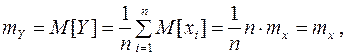(3)

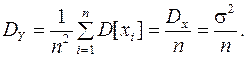(4)

Т. о. 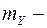не зависит от числа опытов 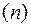, а дисперсия при больших 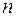может стать сколь угодно малой, т.е. СВ 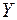ведет себя почти не как случайная. Это свойство и устанавливает теорема Чебышева.

При достаточно большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности к ее математическому ожиданию.

Говорят что СВ 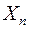сходится по вероятности к величине 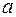, если при увеличении 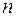вероятность того, что 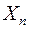и 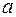будут сколь угодно близки, неограниченно приближается к единице, а это значит, что при достаточно большом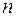

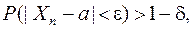(5)

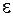где и 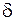– произвольно малые положительные числа. Запишем аналогично теорему Чебышева:

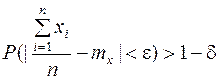. (6)

Обобщенная теорема Чебышева

Пусть 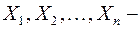независимые случайные величины с соответствующими математическими ожиданиями и дисперсиями, т.е. 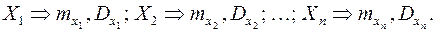И если все дисперсии ограничены сверху одним и тем же числом 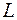таким, что

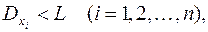то при возрастании 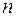среднее арифметическое наблюденных значений величин 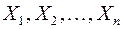сходится по вероятности к среднему арифметическому их математических ожиданий:

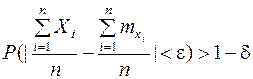. (7)

Теорема Маркова

Если имеются зависимые СВ 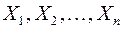и, если при 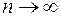справедливо соотношение 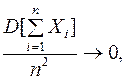то среднее арифметическое наблюденных значений СВ 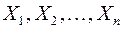сходится по вероятности к среднему арифметическому их математических ожиданий.

Теорема Бернулли

Пусть производится 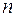независимых опытов, в каждом из которых может произойти или не произойти событие 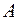, вероятность которого в каждом опыте равна 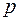. Теорема Бернулли утверждает, что:
при неограниченном увеличении числа опытов 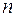частота события 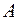сходится по вероятности к его вероятности .

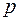Обозначим частоту события 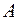в 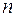опытах через 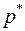тогда теорему Бернулли можно записать в виде формулы:

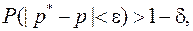(8)

где 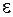и δ – сколько угодные малые положительные числа.

Упражнения:

1. Случайная величина X задана функцией распределения

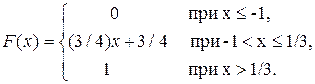
Найти вероятность того, что в результате испытания величина X примет значение, заключённое в интервале (0, 1/3).

2. Случайная величина X задана на всей оси O x функцией распределения F(x) = 1/2 + (arctg x)/π. Найти вероятность того, что в результате испытания величина X примет значение, заключённое в интервале (0, 1).

3. Дана функция распределения непрерывной случайной величины X

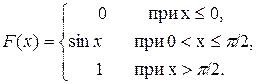
Найти плотность распределения f(x).

4. Дана функция распределения непрерывной случайной величины X

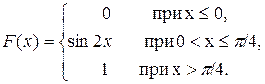
Найти плотность распределения f(x).

5. Случайная величина X задана функцией распределения

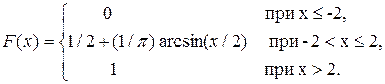
Найти вероятность того, что в результате испытания величина X примет значение, заключённое в интервале (-1, 1).

6. Случайная величина X задана функцией распределения

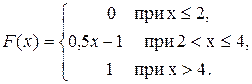
Найти вероятность того, что в результате испытания величина X примет значение: а) меньшее 0,2; б) меньшее трёх; в) не меньшее трёх; г) не меньшее пяти.

7. Случайная величина X задана функцией распределения

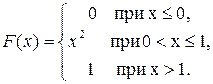
Найти вероятность того, что в результате четырёх независимых испытаний величина X ровно три раза примет значение, принадлежащее интервалу (0,25; 0,75).

8. Дискретная случайная величина X задана законом распределения

X
p	0,5	0,2	0,3

Найти функцию распределения F(x) и начертить её график.

9. Дискретная случайная величина X задана законом распределения

X
p	0,2	0,1	0,4	0,3

Найти функцию распределения F(x) и начертить её график.

10. Непрерывная случайная величина X задана плотностью распределения f(x)=(3/2)sin3 x в интервале (0; π/3); вне этого интервала f(x)=0. Найти вероятность того, что X примет значение, принадлежащее интервалу (π/6; π/4).

11. Задана плотность распределения непрерывной случайной величины X:

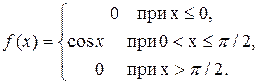
Найти функцию распределения F(x).

12. Задана плотность распределения непрерывной случайной величины X:

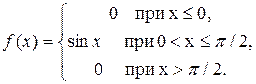
Найти функцию распределения F(x).

13. Задана плотность распределения непрерывной случайной величины X:

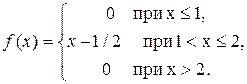
Найти функцию распределения F(x).

14. Задана плотность распределения непрерывной случайной величины X:

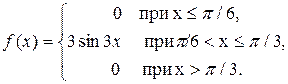
Найти функцию распределения F(x).

15. Случайная величина X задана на всей оси O x функцией распределения F(x)=1/2+(1/π)arctg(x /2). Найти возможное значение x ₁, удовлетворяющее условию: с вероятностью 1/4 случайная величина X в результате испытания примет значение, большее x ₁.

Дата добавления: 2015-10-28