
|
Читайте также: |
Результаты измерений (наблюдений) называют статистическими данными.
Одним из основных способов сбора статистических данных является выборочный метод.
Совокупность всех возможных значений, или реализаций, исследуемых случайных величин называется генеральной совокупностью. Она может состоять из конечного или бесконечного множества значений, называемых элементами генеральной совокупности.
Выборочной совокупностью (или просто выборкой) называется совокупность элементов случайно отобранных из генеральной совокупности.
Объемом совокупности (генеральной или выборочной) называют число элементов этой совокупности.
Метод, основанный на том, что по данным обследования выборки, выделенной из генеральной совокупности, делается заключение о всей генеральной совокупности, называется выборочным методом.
Основное требование к выборке: она должна хорошо представлять генеральную совокупность, т.е. быть репрезентативной (представительной). Выборка будет репрезентативной, если её осуществлять случайным образом.
При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяются на повторные и бесповторные.
Повторной называют выборку, при которой отобранный элемент (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный элемент в генеральную совокупность не возвращается.
Кроме того, различают следующие способы составления выборки: а) простой (случайный), б) механический, в) типический, г) серийный.
Так, если занумеровать все элементы генеральной совокупности и затем изготовить карточки с такими же номерами, тщательно перемешать их и отобрать пачку карточек, то элементы генеральной совокупности с номерами извлечённых карточек образуют простую (случайную) выборку. Здесь возможно повторная и бесповторная выборка.
Предположим теперь, что генеральную совокупность разбили на несколько неперекрывающихся групп и из каждой группы отобраны в случайном порядке объекты. Это типический способ (районированная или стратифицированная выборка) составления выборки. Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности. Например, при определении рейтинга кандидатов в президенты на выборах страну делят на округа и в каждом округе определяется рейтинг кандидатов в президенты.
Наконец, серийная (гнездовая или кластерная) выборка образуется следующим образом. Генеральная совокупность делится на неперекрывающиеся группы. После этого случайным образом отбираются некоторые группы. Полученная выборка будет серийной.
На практике часто применяется комбинированный отбор, при котором сочетаются указанные выше способы.
Как правило, результаты эксперимента или наблюдения дискретных случайных величин (первичные данные) сводятся в таблицу, в первой строке которой записывается номер i эксперимента, а во второй – соответствующий признак x i, называемый вариантой случайной величины. Таблицы такого вида называются статистическими рядами несгруппированных данных. Таблица может включать данные о нескольких признаках (несколько видов вариант), но часто ограничиваются данными об одном признаке.
Ранжированием называется расположение элементов совокупности в порядке возрастания или убывания величины соответствующих им вариантов.
Статистический ряд, расположенный по возрастанию вариант, называется вариационным рядом.
Ранжированный перечень содержит список элементов совокупности упорядоченный по возрастанию. Каждому элементу (и соответствующему ему варианту) приписан ранг – номер занимаемого им места. Одинаковые варианты получают одинаковый ранг.
Дискретной группировкой называется распределение совокупности вариантов по группам, содержащим одинаковые варианты.
Число, показывающее сколько раз (как часто) некоторый вариант x i встречается в совокупности, называется частотой n i (абсолютной частотой) данного варианта. Сумма всех частот равняется количеству элементов совокупности (объему выборки), т.е.
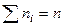 . (1)
. (1)
Относительной частотой (частостью) 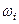 некоторого варианта x i называется доля этого варианта в общем количестве данных, т.е. отношение частоты к объему выборки:
некоторого варианта x i называется доля этого варианта в общем количестве данных, т.е. отношение частоты к объему выборки:
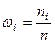 . (2)
. (2)
Для удобства относительную частоту часто выражают в процентах, умножая результат на 100.
Соответствие между вариантами и их частотами (относительными частотами) называется статистическим распределением выборки.
Одновременно с понятием частоты и относительной частоты в сгруппированных совокупностях применяются понятия накопленной частоты и относительной частоты.
Накопленной частотой 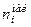 некоторого варианта x i называется количество элементов ранжированной в порядке возрастания совокупности, имеющих значение признака меньше или равное данному:
некоторого варианта x i называется количество элементов ранжированной в порядке возрастания совокупности, имеющих значение признака меньше или равное данному:
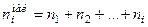 . (3)
. (3)
Накопленной относительной частотой 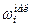 некоторого варианта x i называется отношение накопленной частоты этого варианта
некоторого варианта x i называется отношение накопленной частоты этого варианта 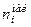 к объему выборки:
к объему выборки:
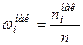 . (4)
. (4)
В тех случаях, когда число различных вариантов в совокупности велико или вариация является непрерывной при обработке статистических данных используется интервальная группировка.
Интервальной группировкой называется распределение совокупности вариантов на группы вариантов, лежащих в определённых границах.
Статистическая таблица, получаемая в результате интервальной группировки, называется интервальным вариационным рядом.
Максимальное значение варианта для конкретного интервала называется верхней границей x i(max), а минимальное – нижней границей интервала x i(min). Величина интервала – разность между верхней и нижней границами интервала:
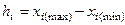 . (5)
. (5)
Ещё одним способом группировки совокупности является комбинационная группировка – распределение совокупности на группы по сочетанию (комбинации) нескольких признаков.
Для наглядности рассмотрения статистических данных ряды распределения представляются в графической форме. Наиболее широко используются следующие виды графического изображения вариационных рядов в прямоугольной системе координат: полигон, гистограмма, кумулятивная кривая.
Полигоном (многоугольником) распределения называется графическое изображение вариационного ряда в прямоугольной системе координат, при котором величины признака (варианты) x i откладываются на оси абсцисс, а частоты (или относительные частоты) на оси ординат.
Таким образом, полигон частот представляет собой ломанную, отрезки которой соединяют точки M 1(x 1, n 1), M 2(x 2, n 2), …, M k(x k, n k). Полигон относительных частот есть ломанная, отрезки которой соединяют точки M 1(x 1, ω 1), M 2(x 2, ω 2), …, M k(x k, ω k). Крайние точки М 1 и М 2, если они не лежат на оси абсцисс, обычно также соединяют со смежными точками M 0(x 0, 0), M k+1(x k+1, 0).
Гистограммой вариационного ряда называется графическое изображение интервального вариационного ряда в виде прямоугольников, основания которых – отрезки оси абсцисс, соответствующие интервалам изменения признака, а высоты пропорциональны плотностям частот (или относительных частот) интервалов.
Кумулятивная кривая (кумулята) это графическое изображение вариационного ряда, составленное по последовательно суммированным, т.е. накопленным частотам (или относительным частотам).
Эмпирической функцией распределения (или функцией распределения выборки) называется функция 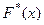 , определяющая для каждого значения x относительную частоту события X< x:
, определяющая для каждого значения x относительную частоту события X< x:
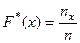 , (6)
, (6)
где nx – число вариант, меньших x; n – объем выборки.
Из определения эмпирической функции следует, что 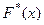 обладает всеми свойствами функции распределения F(x), а именно:
обладает всеми свойствами функции распределения F(x), а именно:
1) значения функции 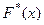 принадлежат интервалу [0,1];
принадлежат интервалу [0,1];
2) 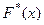 - неубывающая функция;
- неубывающая функция;
3) если а – наименьшая, а b – наибольшая варианта, то 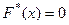 при
при 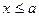 и
и 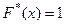 при
при 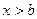 .
.
Упражнения:
1. Построить вариационный ряд, начертить полигон и кумулятивную кривую относительных частот для следующего распределения: 39, 41, 40, 42, 41, 40, 42, 44, 40, 43, 42, 41, 43, 39, 42, 41, 42, 39, 41, 37, 43, 41, 38, 43, 42, 41, 40, 41, 38, 44, 40, 39, 41, 40, 42, 40, 41, 42, 40, 40, 41, 38, 44, 40, 39, 41, 40, 42, 40, 41, 42, 40, 40, 41, 38, 44, 40, 39, 41, 40, 42, 40, 41, 42, 40, 43,38,39,41,41, 41.
2. Наблюдения за результатами некоторого эксперимента дали следующие результаты:
21, 30, 39, 31, 42, 34, 36, 30, 28, 30, 33, 24, 31, 40, 31, 33, 31, 27, 31, 45, 31, 34, 27, 30, 48, 30, 28, 30, 33, 46, 43, 30, 33, 28, 31, 27, 31, 36, 51, 34, 31, 36, 34, 37, 28, 30, 39, 31, 42, 37.
Построить по этим данным интервальный вариационный ряд с равными интервалами величиной hi =4 и начертить гистограмму частот.
3. Построить эмпирическую функцию распределения и её график по данным выборки:
| xi | |||
| ni |
4. В результате анализа состава рубрик сайтов в сфере СМИ были получены следующие данные:
| № п/п | Наименование рубрики, подрубрики | Порядковые номера сайтов | |
| новости | 1, 5, 8, 10, 12-15, 17-24, 26-28, 30 | ||
| в мире | 10, 13, 15-17, 25 | ||
| О нас | 1-9, 17-20, 22-25, 27, 29, 30 | ||
| поиск | 5, 8-20, 24, 25, 27-30 | ||
| Реклама | 3, 7-9, 11, 13-17, 19-23, 25-27, 29 | ||
| контакты | 6, 11, 15, 16, 18, 19, 21, 23-30 | ||
| Архивы | 1-4, 8, 9, 12, 18-23, 28, 30 | ||
| Культура | 5, 8, 12, 15-17, 22, 25, 30 | ||
| Форум | 2, 3, 6, 8, 16-19, 23, 25-30 | ||
| Обратная связь | 1, 5, 8, 10, 14, 16-23, 30 | ||
| Политика | 5, 8, 10, 12, 13, 15-17, 22, 25, 27, 30 | ||
| новости о нас | 11, 14, 25-27 | ||
| экономика | 8, 10, 12, 13, 15-17, 21, 22, 25, 27, 30 | ||
| досуг | 14, 16, 22, 30 | ||
| Спорт | 5, 8, 12, 15-17, 21, 22, 25, 27, 30 | ||
| подписка | 1, 10, 14, 15, 16, 18, 21, 22, 24, 30 | ||
| Календарь | 1, 5, 15, 28 | ||
| Происшествия | 5, 8, 13, 15-17, 22, 25 | ||
| история | 7, 20, 25, 28 | ||
| партнеры | 10, 13, 15, 17, 19, 20, 24, | ||
| СМИ о нас | 8, 18, 23, 25 | ||
| Статьи | 1, 2, 15, 27-30 | ||
| справочники | 22, 24, 27, 29, | ||
| Сотрудники | 4, 8, 20, 21, 25 | ||
| вакансии | 14-16, 21, 23, 25 | ||
| гостевая книга | 7, 9, 13, 14, 22, 27 | ||
| интервью | 7, 15, 18, 20, 21, 23 | ||
| Блоги | 1, 8, 22, 24, 26 | ||
| Общество | 5, 8, 10, 12, 13, 15-17, 22, 25, 30 | ||
| пресс-центр | 11, 12, 14, 15, 22 | ||
| программа передач | 13, 18, 19, 23, 25 | ||
| руководство | 13, 14, 19, 23, 25, | ||
| спецпроекты | 15, 20, 22, 23 | ||
| в эфире | 8, 11, 18, 20, 23, 25, 26 | ||
| Прайс-лист | 6, 14, 19, 21 | ||
| Программы | 6, 7, 11, 13, 19, 25, 26 | ||
| Музыка | 8, 20, 23, 26 | ||
| Опрос | 1, 5, 16, 21 | ||
| Фотогалерея | 5, 6, 8, 16, 21, 22, 27 |
Провести дискретную группировку и ранжирование представленной совокупности. Данные представить в виде таблиц 1 и 2.
Таблица 1
Частота встречаемости рубрик, подрубрик сайта
| № п/п | Наименование рубрики, подрубрики | Порядковые номера сайтов | Частота встречаемости | |
| абс | % | |||
Таблица 2
Ранжированная частота встречаемости рубрик, подрубрик сайта
| Ранг | Наименование рубрики, подрубрики | Частота встречаемости (абс.) |
5. Дана выборка из 60 элементов: 1, 4, 3, 5, 3, 5, 0, 5, 0, 4, 1, 1, 4, 2, 3, 1, 5, 3, 1, 4, 3, 0, 6, 1, 2, 2, 4, 2, 4, 3, 3, 1, 4, 3, 5, 4, 4, 5, 2, 1, 2, 10, 4, 1, 1, 4, 5, 2, 3, 2, 4, 5, 4, 1, 3, 2, 1, 3, 9, 5. Требуется построить (вычислить) по данному распределению выборки:
1) вариационный ряд частот и относительных частот;
2) полигон частот и полигон относительных частот;
3) гистограмму относительных частот;
4) кумулятивную кривую относительных частот;
5) эмпирическую функцию распределения и её график.
6. Дана выборка, представленная в задании № 5. Требуется построить (вычислить) по данному распределению выборки:
1) интервальный вариационный ряд частот и относительных частот из 5 интервалов;
2) полигон частот и полигон относительных частот;
3) гистограмму относительных частот;
4) кумулятивную кривую относительных частот;
5) эмпирическую функцию распределения и её график.
7. В результате анализа состава рубрик сайтов Интернет-магазинов были получены следующие данные:
| № п/п | Наименование рубрики, подрубрики | Порядковые номера сайтов | |
| О магазине | 1,2,3,4,6,7,8,9,10,12,13,15,17,18,19,20,21,22,25,26,27,28,30 | ||
| Доставка и оплата | 1,2,3,4,5,6,9,10,11,14,15,16,17,18,19,20,21,22,24,25,26,27,28 | ||
| Как заказать товар? | 1,2,4,5,6,7,9,10,11,13,17,19,20,21,24,25,26 | ||
| Ваши покупки (корзина) | 1,2,3,4,5,7,8,9,10,11,12,13,14,17,18,19,20,21,22,23,25,26,27,29 | ||
| Заказ оптом | 1,3,17,20,21,28,29 | ||
| Каталог (прайс-лист) | 2,3,4,5,6,7,8,10,11,12,13,14,15,16,18,19,20,21,23,24,25,26,27,28,29,30 | ||
| Новинки | 2,4,5,6,8,10,12,16,18,19,22,23,24,26,27,28 | ||
| Скидки | 2,4,5,6,7,8,10,14,18,20,22,26,28,30 | ||
| Спец. предложения | 2,8,11,12,13,14,17,19,20,21,22,23,24,26,27,28,29,30 | ||
| Новости | 2,3,4,5,6,7,8,9,12,13,14,16,18,20,21,22,25,26,29,30 | ||
| Контакты | 1,2,3,4,5,6,7,8,9,10,13,14,15, 17,19,20,22,23,24,25,28,29,30 | ||
| Гостевая книга | 3,5,6,9,13,14,19,21,23,24,25, 28 | ||
| Сайты регионов | 3,6,16,20,26,28 | ||
| Сотрудничество | 3,4,6,8,10,12,15,17,18,20,22, 25,28,29 | ||
| Вакансии | 1,2,3,4,7,11,16,18,21,23,28 | ||
| Сервис (установка) | 3,5,10,20,21,26,27 | ||
| Ссылки | 4,6,9,10,18 | ||
| Соглашение | 5,9,10 | ||
| Карта сайта | 5,11,23,28,30 | ||
| Подписка | 5,6,21 | ||
| Рейтинг | 1,6,13,18,22,23,24 | ||
| Условия использования | 6,28 | ||
| Техподдержка | 6,7,8 | ||
| Форум | 7,8,10,21,23,26,28,29 | ||
| Советы покупателям | 6,8,10,11,13,14,17,18,19,20,22,24,25,26,27,28,29 | ||
| Регистрация | 1,2,3,4,5,6,7,8,9,10,11,13,16, 17,18,19,20,22,24,26,27 | ||
| Статьи | 7,9,26 | ||
| Личная информация | 7,8,9,10,11,12,17,22,27 | ||
| Гарантия | 9,16,19,20,21,27,28,30 | ||
| Другое | 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30 |
Провести дискретную группировку и ранжирование данной совокупности. Данные представить в виде таблиц 1 и 2 из задания № 4.
8. Построить дискретный вариационный ряд и начертить полигон, гистограмму и кумулятивную кривую относительных частот для следующего распределения: 30, 32, 31, 33, 32, 31, 33, 35, 31, 34, 33, 32, 34, 30. 33, 32, 33, 30, 32, 28, 34, 32, 29, 34, 33, 32, 31, 32, 29, 35. 31, 30, 32, 31, 33, 31, 32, 33, 31, 34, 29, 30, 32, 32, 33.
9. В результате анализа состава рубрик образовательных порталов были получены следующие данные:
| № п/п | Наименование рубрики, подрубрики | Порядковые номера сайтов | |
| Новости | 1,2,3,5,8,10-28,30 | ||
| Законодательство | 1,3 | ||
| Интерактив | 1,3,4,5,6-12,14,15,16,18,19,21-30 | ||
| От аспиранта к профессору | 1,24,28 | ||
| Из истории образования | 4,7,18,19,21-30 | ||
| Экономика | |||
| Статьи | 5,8,10,12,14,15,17,19,22,25,27,29 | ||
| Рубрикатор | 4,11,12,13,16,18,20,21,23 | ||
| Глоссарий (Словари) | 1,2,3 | ||
| Организации (справочная информация) | 1,22,25 | ||
| Гос. премии, гранты, конкурсы | 6,7,8,13,15,17,27,28 | ||
| Гос. образовательные стандарты | 1,2 | ||
| Каталог образовательных интернет-ресурсов | 1,2,4,5,7,11,13 | ||
| Карта сайта | 4,5,6,8,13,14,20 | ||
| Курсы лекций | 6,9,12,16,19,23 | ||
| Нормативные документы | 1,2,5,6,7 | ||
| Номенклатура специальностей | 4,18,22,26,28 | ||
| Тренинги | 8,12,16,24,29 | ||
| Учреждения; техникумы, вузы | 1,2,10,16, | ||
| Интернет-консультации по ЕГЭ | 3,2,5,10 | ||
| компьютерные программы | 1,2,12,23 | ||
| Коллекции | 1,2,17 | ||
| Периодические издания; | 1,2,3,6,8,10 | ||
| Студенческие работы | 4,5,9,12,18,23,26,30 | ||
| Образовательные CD/DVD. | 1,24,26 | ||
| Мероприятия | 1,2,3 | ||
| Дистанционное обучение | 1,6,8 | ||
| учебные программы | 1,2,3,5,6,7,10,11,13,21,24,23,26 | ||
| Библиотеки | 1,2,3,5,6,8-17,20,22 | ||
| Персоналии | 1,10 | ||
| Картографический сервис | 1,26 | ||
| О портале | 1-30 | ||
| Иллюстративные материалы | 4,9 | ||
| Уровни образования | 1,3 | ||
| Государственное и муниципальное управление | |||
| Социология |
Провести дискретную группировку и ранжирование данной совокупности. Данные представить в виде таблиц 1 и 2 из задания № 4.
Дата добавления: 2015-10-28; просмотров: 120 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Показательное распределение | | | Числовые характеристики выборки |