Производные по направлениям и субдифференциалы

Выпуклые функции в общем случае могут быть недифференцируемы в обычном смысле (например, f(x) = |x| недифференцируема в точке х = 0).

Определение. Производной по направлению p(p Rⁿ, p 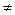0) функции f в точке х называется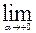 и обозначается f ’(x, p) или 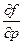(х).

Отметим, что если f(x) дифференцируема в точке х, то f ’(x, p) = (f ’(x),p), где

f ’(x) = - градиент функции f в точке х.

Теорема Радемахера. Всякая выпуклая функция является дифференцируемой почти всюду (за исключением множества лебеговой меры нуль) на открытом множестве Х dom f.

Теорема. Пусть f(x) – выпуклая функция на Rⁿ. Тогда для любой точки х int(dom f) существует и конечна производная функции f по любому направлению pRⁿ.

Для выпуклых функций можно определить понятие субградиента, которое заменяет обычное понятие градиента гладкой функции в задачах на экстремум.

Определение. Вектор g называется субградиентом функции f в точке х⁰ dom f, если

f(x) – f(x⁰) 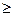(g, x – x⁰) для любых х Rⁿ.

Множество всех субградиентов функции f в точке х⁰ называется субдифференциалом функции f и обозначается f(x⁰).

Замечание. В определении субградиента не требуется выпуклости функции и можно вычислить субградиент в заданной точке и для произвольной функции. Однако для выпуклой функции, определённой на открытом выпуклом множестве, всегда существует хотя бы один субградиент в любой точке множества, т.е. её субдифференциал является непустым множеством. Для произвольной функции это не так.

Дата добавления: 2015-09-01