Читайте также:
|
Можно показать, что если f(x) выпуклая функция, то
1) вектор g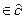 
f(x0) является внешней нормалью опорной гипреплоскости к множеству уравня M(f) функции f в точке х0, где M(f) = {x 
Rn| f(x) 
f(x0)};
2) вектор (g, - 1)Rn+1, где g 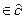f(x0), является внешней нормалью опорной гиперплоскости, проведённой к надграфику функции f в точке (x0, f(x0)) (в частности, если x R, то g есть тангенс угла наклона опорной прямой, проведённой к надграфику функции f);
3) для функции f: R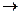 
R 
f(x) = [f ’(x – 0), f ’(x + 0)].
Дата добавления: 2015-09-01; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Производные по направлениям и субдифференциалы | | | Свойства субдифференциала выпуклой функции |