Свойства выпуклых функций

1. Функция f выпукла на выпуклом множестве Х в том и только в том случае, если справедливо неравенство Иенсена:

f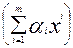

для любого m, любых xⁱ X, i = 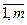и любых α_i 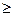0, i = 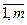, = 1.

2. Пусть f_i, i = 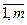- выпуклые функции на выпуклом множестве Х, тогда

а) f(x) = 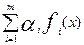- выпуклая функция если α_i 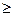0, i = .

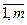б) f(x) = f_i(x) – выпуклая функция, где I – произвольное множество индексов.

3. Пусть g – выпуклая функция на выпуклом множестве Х Rⁿ, : R 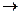R – неубывающая выпуклая функция. Тогда функция f(x) = (g(x)) выпукла на Х.

4. Пусть - выпуклая функция на R^m, A – матрица размера m n, b R^m. Тогда функция

f(x) = (Ax + b) выпукла на Rⁿ.

5. Пусть f – выпуклая функция на Rⁿ. Тогда f непрерывна в любой внутренней точке множества dom f.

Замечание. Если функция f выпукла и конечна на выпуклом множестве Х, тогда f непрерывна в любой внутренней точке множества Х (т.е. функция f может иметь разрывы только на границе множества Х).

Дата добавления: 2015-09-01