
Читайте также:
|
1. Пересечение произвольного числа выпуклых множеств выпукло, т.е. если Xi – выпуклое множество, i  I, где I – произвольный набор индексов, то X =
I, где I – произвольный набор индексов, то X =  Xi – выпукло.
Xi – выпукло.
2. Если множества X1 и X2 – выпуклы, а1 и а2 – произвольные вещественные числа, то множество X = а1X1 + а2X2 – выпукло, где
а1X1 + а2X2 = {x  Rn: x = a1x1+a2x2, x1
Rn: x = a1x1+a2x2, x1  X1, x2
X1, x2  X2}.
X2}.
3. Если X – выпуклое множество и точки х1,х2,…,хm принадлежат Х, то Х содержит все их выпуклые линейные комбинации.
4. Выпуклая оболочка произвольного множества Х совпадает с множеством всех выпуклых комбинаций точек из Х.
Замечание. Из свойств 3 и 4 следует критерий выпуклости: множество Х выпукло в том и только в том случае, если оно содержит все выпуклые комбинации своих точек.
5. Пусть Х – выпуклое множество, тогда 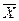 и int X – выпуклые множества.
и int X – выпуклые множества.
Важную роль в теории экстремальных задач играют теоремы отделимости.
Теорема о разделяющей гиперплоскости. Пусть Х – замкнутое, выпуклое множество, а – точка в пространстве Rn, а 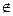 Х. Тогда существует гиперплоскость с нормалью р
Х. Тогда существует гиперплоскость с нормалью р 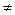 0 такая, что
0 такая, что
(р,а)>с и (р,х)  с для
с для 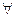 х
х  Х.
Х.
Геометрически существование разделяющей гиперплоскости можно продемонстрировать следующим образом.
 Замечание. Если не выполнены условия теоремы, то разделяющую гиперплоскость провести можно не всегда (см. рис. 3)
Замечание. Если не выполнены условия теоремы, то разделяющую гиперплоскость провести можно не всегда (см. рис. 3)
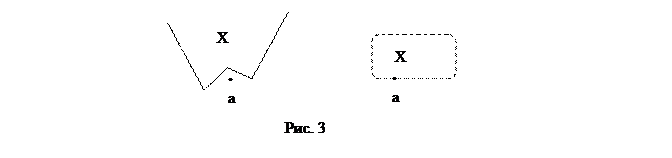
Определение. Гиперплоскость (р,х) = с называется опорной к множеству Х в точке х0  Х, если для
Х, если для 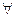 х
х  Х выполняются соотношения
Х выполняются соотношения
(р,х)  с и (р,х0) = с.
с и (р,х0) = с.
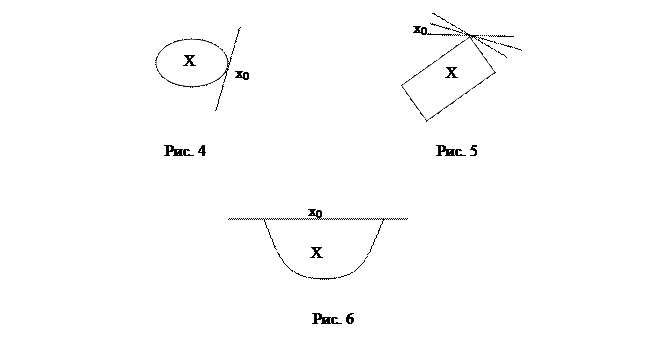
На рис. 4 – 6 приведены примеры взаимного расположения выпуклого множества Х и гиперплоскостей, опорных к Х в точке х0.
Теорема об опорной гиперплоскости. В любой граничной точке х0 к выпуклому замкнутому множеству Х можно построить опорную гиперплоскость.
Следует заметить, что для невыпуклых множеств это неверно: не через всякую граничную точку можно провести опорную гиперплоскость; так, на рис. 7 изображено множество Х, для которого через точку х0 нельзя провести опорную гиперплоскость.
 Теорема отделимости. Если Х1 и Х2 – выпуклые непересекающиеся множества, то существует вектор р
Теорема отделимости. Если Х1 и Х2 – выпуклые непересекающиеся множества, то существует вектор р  Rn, р
Rn, р 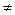 0 такой, что (р,х1)
0 такой, что (р,х1)  (р,х2) для любых х1
(р,х2) для любых х1  Х и х2
Х и х2  Х2.
Х2.
Определение. Пусть f: Rn  R. Множество пар y
R. Множество пар y  R и x
R и x  Rn таких, что f(x)
Rn таких, что f(x)  y называется надграфиком функции f и обозначается epi f.
y называется надграфиком функции f и обозначается epi f.
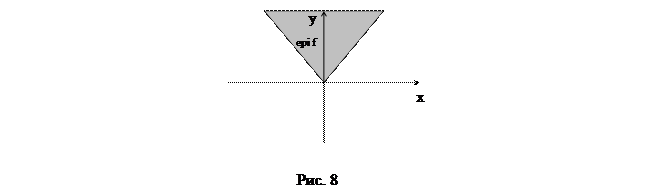
Пример. На рис. 8 изображён надграфик функции f(x) = |x|, область epi f находится над графиком y = |x|.
Определение. Проекцией точки а  Rn на множество Х
Rn на множество Х  Rn называется точка р
Rn называется точка р  Х такая, что
Х такая, что
||p-a||  ||x-a|| для любых х
||x-a|| для любых х  Х и обозначается Рх(а).
Х и обозначается Рх(а).
Теорема. Пусть Х – выпуклое, замкнутое множество, точка а  Rn. Тогда проекция Рх(а) существует и единственна.
Rn. Тогда проекция Рх(а) существует и единственна.
Дата добавления: 2015-09-01; просмотров: 248 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Выпуклые множества | | | Задачи и упражнения |