
Читайте также:
|
1. Функция f(x) выпукла на всём пространстве тогда и только тогда, когда функция g(t) = f(x + tp) одной переменной t  [0,1] выпукла при любых х, р.
[0,1] выпукла при любых х, р.
2. Дважды непрерывно дифференцируемая функция f, определенная на выпуклом множестве Х, выпукла на Х в том и только том случае, если
(f ”(x)y,y) 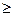 0
0 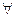 x
x  X,
X, 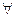 y
y  Rn,
Rn,
т.е. если f ”(x) – матрица вторых производных функции f неотрицательно определена в любой точке х множества Х.
3. Пусть f(x) дважды непрерывно дифференцируема на Х, Х – выпуклое множество. Тогда f(x) – сильно выпуклая функция с параметром 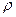 >0 на Х в том и только в том случае, если
>0 на Х в том и только в том случае, если
(f ”(x)y,y) 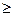
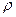 ||y||2 для
||y||2 для 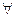 y
y  Rn и
Rn и 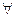 х
х  Х.
Х.
Замечание. Выяснить, является ли эрмитова матрица А неотрицательно определённой можно, использовав один из следующих критериев.
1) Матрица А неотрицательно определена (А 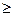 0) тогда и только тогда, когда все её собственные значения неотрицательны.
0) тогда и только тогда, когда все её собственные значения неотрицательны.
2) А 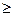 0 в том и только в том случае, если все главные миноры (т.е. определители вида
0 в том и только в том случае, если все главные миноры (т.е. определители вида
 …ik = det
…ik = det  ,
,
где 1  i1<i2<…<ik
i1<i2<…<ik  n, k =
n, k =  ) – неотрицательны.
) – неотрицательны.
В теории решения экстремальных задач играют важную роль следующие теоремы.
Теорема. Пусть f(x) – выпуклая функция на выпуклом множестве Х. Тогда любая точка локального минимума f(x) на Х является точкой глобального минимума.
Теореме. Пусть f(x) – строго выпуклая функция на выпуклом множестве Х и множество её точек минимума Х* непусто. Тогда Х* состоит из единственной точки.
Теорема. Пусть f(x) – непрерывно сильно выпуклая функция с параметром 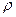 >0 на Х, Х – замкнутое, выпуклое, непустое множество. Тогда решение задачи f(x)
>0 на Х, Х – замкнутое, выпуклое, непустое множество. Тогда решение задачи f(x) 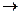 min, х
min, х  Х существует и единственно.
Х существует и единственно.
Дата добавления: 2015-09-01; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства выпуклых функций | | | Задачи и упражнения |