Выпуклые множества

Элементы выпуклого анализа

Методические указания к практическим занятиям

По курсу «Методы оптимизации»

Челябинск 1998

Выпуклые множества

Будем рассматривать векторы x, принадлежащие n-мерному пространству Rⁿ . Заметим, что введенные ниже понятия можно распространить на произвольное линейное нормированное пространство Е. Большая часть приведенных ниже теорем при некоторых дополнительных предположениях будут также справедливы в пространстве Е. Однако в целях простоты и наглядности изложения ограничимся случаем пространства Rⁿ.

Определение. Множество X Rⁿ называется выпуклым, если для любых точек x X и y Y и любого числа [0,1] точка z = x +(1- )y также принадлежит множеству X.

Таким образом, по определению любое выпуклое множество вместе с каждыми своими двумя точками x и y содержит весь отрезок, их соединяющий.

Упражнение. Какие из представленных на рис. 1 множеств являются выпуклыми?

Определение. Будем говорить, что точка x является выпуклой линейной комбинацией точек x₁,x₂,…,x_m, если существуют числа α₁,α₂,…,α_m такие, что

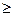α_i 0,i = 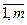, α₁+α₂+…+α_m=1 и x=α₁x₁+α₂x₂+…+α_mx_m.

Определение. Пересечение всех выпуклых множеств, содержащих данное множество X, называется выпуклой оболочкой множества X и обозначается Conv X.

Пусть в Rⁿ определенно (x,y) – скалярное произведение векторов x и y, ||x|| = 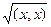- норма вектора x.

Определение. Точка x называется внутренней точкой множества X, если существует 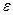>0 такое, что множество O_ε(x)={y Rⁿ: ||x-y|| ε} содержится в X.

Определение. Множество внутренних точек множества X называется внутренностью множества X и обозначается int X.

Определение. Совокупность всех предельных точек множества X называется замыканием X и обозначается .

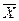Определение. Замыкание выпуклой оболочки множества X называется замкнутой выпуклой оболочкой X и обозначается .

Определение. Точка x называется граничной точкой множества X, если любая её окрестность содержит как точки, принадлежащие X, так и точки не принадлежащие X. Множество всех граничных точек множества X называется его границей и обозначается X.

Дата добавления: 2015-09-01