Задачи и упражнения. 1. Построить выпуклую функцию, определённую на [0, 1], которая не имеет производной в

1. Построить выпуклую функцию, определённую на [0, 1], которая не имеет производной в бесконечном числе точек.

2. Следует ли из существования конечной производной по любому направлению дифференцируемость выпуклой функции? Рассмотреть пример

.

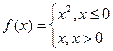3. Вычислить производную по направлению p R² в точке (0, 0) функции

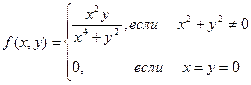. Показать, что в этой точке существует производная по любому направлению, однако функция не является непрерывной в данной точке. Почему такая ситуация невозможна для выпуклой функции?

Указание.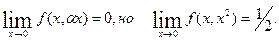

4. Привести пример функции, для которой субдифференциал в некоторой точке является пустым множеством.

5. Доказать, что субдифференциал f(x⁰) – выпуклое, замкнутое множество для любой точки x⁰ X.

6. Доказать, что если h(x) = αf(x), α > 0, то h(x) = α f(x) для х Х.

7. Доказать, что если f(x) = |h(x)|, x Rⁿ, где h(x) – непрерывная функция и h(x) = 0, тогда нулевой вектор принадлежит f(a) (0 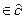f(a)).

8. Пусть f – выпуклая функция на R, x⁰ int(dom f), f(x⁰) = {a}, где a R. Показать, что f дифференцируемая функция в точке x⁰ и f ’(x⁰) = a.

9. Пусть f: Rⁿ 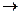R₊ - собственная функция и f(x) 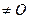для любого x dom f. Доказать, что f – выпуклая функция.

10. Найти субдифференциалы и производные по направлениям следующих функций:

а) f(x) = |x – 1| + |x + 1+, x R;

б) f(x) = max{x², x + 2};

в) f(x) = max{2x – 3, 0.5x + 1, - x + 1};

г) f(x) = max{|x|, |x – 1|};

д) f(x) =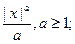

е) f(x) = |x₁ + x₂|, x R²;

ж) f(x₁, x₂) = |2x₁ – 3x₂|;

и*) f(x) =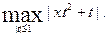

---

Дата добавления: 2015-09-01