Свойства субдифференциала выпуклой функции

Пусть f(x) – выпуклая функция, определённая на открытом выпуклом множестве Х dom f. Тогда справедливы следующие утверждения.

1. Субдифференциал f(x⁰) – непустое выпуклое, замкнутое и ограниченное множество для любой точки х⁰ Х.

2. Если f(x) – дифференцируемая функция в точке х⁰ Х, то

f(x⁰) = {f ’(x⁰)}.

3. Пусть h(x) = αf(x), α > 0, тогда

h(x) = αf(x) для 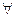x X

4. Пусть f(x) = f₁(x) + f₂(x), где f₁(x) и f₂(x) – выпуклые на Х функции, тогда

f(x) = f₁(x) + f₂(x) для 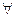х Х.

5. Пусть функции f₁, f₂, …,f_m – выпуклые функции, определённые на Х, и f(x) = 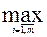f_i(x). Тогда

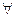f(x) = conv для х Х,

где I(x) = {i = 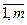: f_i(x) = f(x)}.

6.Производная функции f в произвольной точке по любому направлению p Rⁿ, p 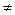0 существует и

f ’(x, p) = (g, p).

Замечание. Требование открытости множества Х существенно. Если Х – произвольное выпуклое множество, то в его граничных точках свойства 1 – 6 будут выполняться только при некоторых дополнительных предположениях.

В общем случае вычисление субдифференциала f(x) задача непростая. Один из инструментов решения этой задачи даёт теорема Кларка.

Теорема Кларка. Пусть x⁰ int dom f, f(x) – выпуклая функция на Rⁿ, Q – множество точек пространства Rⁿ, в которых функция f(x) недифференцируема, {x^k} – произвольная последовательность, сходящаяся к x⁰(x^k 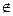Q для любого k), такая, что последовательность сходится. Тогда субдифференциал функции f(x) в точке x⁰ совпадает с выпуклой комбинацией всех пределов последовательностей для всевозможных последовательностей {x^k}, т.е.

f(x⁰) = Conv .

Дата добавления: 2015-09-01