I.6. Работа и теплота. Свойства работы и теплоты.

A – абсолютная работа, Q – теплота. В дальнейшем будем использовать их удельные величины с теми же обозначениями.

Работа бывает не только механической, но и немеханической (например, работа химических реакций).

Работа и теплота – единственные формы передачи энергии. Это одна из формулировок I-го начала термодинамики. Установлено, что внутренняя энергия U является однозначной функцией всей совокупности координат состояния системы, то есть U = U(x₁, x₂,…,x_n).

Если бы это условие не выполнялось, то стал бы возможен вечный двигатель первого рода – двигатель, творящий работу без подвода энергии извне.

Цикл - это круговой процесс, в котором система возвращается в первоначальное состояние. Если цикл идёт по часовой стрелке, то он называется прямым, а если против – обратным.

рис.5. Произвольный прямой обратимый цикл.

Для произвольного обратимого цикла (рис.5)

DU_1-а-2-б-1 = 0 или

(28)

Из математики известно, что равенства вида 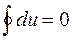означают наличие под знаком интеграла полного дифференциал функции U. В любом произвольном процессе изменение внутренней энергии от состояния 1 до состояния 2 определяется ее начальными и конечными значениями, таким образом внутренняя энергия является функцией состояния:

(29)

Примером функции состояния из другой области является потенциальная энергия E_пот=mgH, величина которой не зависит от траектории подъёма или опускания груза на высоту H.

Ранее было получено I-ое начало термодинамики в общем виде:

Исходя из того, что единственным источником теплоты и работы является внутренняя энергия системы (U), выделим в правой части этого выражения отдельное слагаемое dQ, соответствующее тепловому взаимодействию:

.

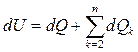Как было установлено в ходе развития науки, для всех взаимодействий, кроме теплового, справедливо соотношение:

dA_k = –dQ_k,

где A_k – абсолютная работа при k-ом взаимодействии (механическая и немеханичекская). Тогда 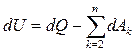. Введем обозначение и окончательно получим I-ое начало термодинамики в обычной форме

dQ = dU + dA (30)

Проинтегрируем уравнение (30) и выразим Q

Q = ∆U + A (30*)

Таким образом, подведенная к системе теплота идет на изменение ее внутренней энергии и на совершение системой абсолютной работы.

Исследуем принадлежность A и Q к функциям состояния. Так как .

Возможны два варианта:

- оба круговых интеграла имеют нулевые значения;

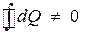- , при и .

Для простоты рассмотрим деформационную систему, которая, как известно, имеет одну (деформационную) степень свободы. Рассмотрим абсолютную работу в произвольном цикле, который совершает эта система.

б

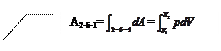
рис.6. Произвольный цикл деформационной системы.

Как известно, геометрический смысл интеграла - это площадь под кривой y = y(x) на отрезке x₁-x₂. Из рис.6. для произвольного цикла видно, что площадь 1-а-2 в общем случае не равна площади под кривой 2-б-1, поэтому

Окончательно и (31)

соответственно, (31*)

Таким образом, A и Q не являются функциями состояния, а являются функциями процесса.

Дата добавления: 2015-09-01