Читайте также:
|
1) Рассмотрим слабые возмущение. При слабом возмущении абсолютная величина относительной разности потенциалов, значительно меньше 1:
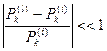(9)
Обозначим через ε бесконечно малую величину разности потенциалов
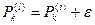(10)
Тогда первое начало термодинамики (5) запишется в следующем виде:
dU = 
= 
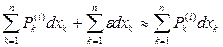(11)
окончательно:
dU =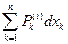 
(12)
Уравнение (12) не содержит информации о направлении протекания процесса, так как принебрегли слагаемым с ε, в знаке которой содержится эта информация.
Это возможно если процессы протекают как в прямом, так и в обратном направлении одинаковым образом, то есть являются обратимыми.
Обратимыми называются процессы, в которых система и окружающая среда проходят через одни и те же состояния как при прямом, так и при обратном направлении.
При слабом возмущении значения термодинамических параметров по всему объёму системы будут практически одинаковыми, как при равновесии, поэтому взаимодействия при малых возмущениях называются равновесными, а процессы, протекающие при этом, являются квазистатическими. В таких процессах системы как бы проходят через непрерывную цепь состояний равновесия. Время, как параметр, в силу квазистатичности в уравнениях не фигурирует. Классическая термодинамика рассматривает только равновесные взаимодействия, поэтому первое начало термодинамики в общем виде записывается как (12), но знак (i) опускается:
dU =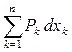 
. (12*)
2) Рассмотрим сильные возмущения. При сильном возмущении абсолютная величина относительной разности потенциалов больше или равна единице:
.
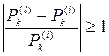Обозначим через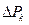 
конечную величину, которой нельзя принебрегать
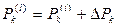
Тогда уравнение (5) запишется в следующем виде
dU =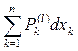 
= 
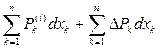
На основании правила знаков для потенциалов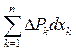 
>0.
Таким образом, изменение U системы при сильном возмущении всегда больше её значения, вычесленного по значениям координаты и потенциала системы.
При сильном возмущении значения термодинамических параметров по объёму системы могут сильно различаться, поэтому такие взаимодействия называются неравновесными, процессы – нестатическими. Время является параметром в уравнениях этих процессов.
Дата добавления: 2015-09-01; просмотров: 176 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| I.2. Теплота, работа, внутренняя энергия. | | | I.4. Состояния системы. Уравнения состояния системы. |