I.1. Основные определения термодинамики.

Система – тело или совокупность тел, являющихся объектов изучения.

Окружающая среда – все остальные тела.

Процесс – изменение физических параметров системы, проявляющиеся в изменении ее термодинамических параметров состояния.

Например, если объектом изучения является газ в цилиндре под поршнем, то системой является газ, а все остальное – окружающая среда.

Координатой состояния системы называется величины, которая всегда из­меняются при наличии данного взаимодействия, и остается постоянной при его отсутствии. Другими словами, координата состояния системы – это индикатор наличия или отсутствия данного взаимодействия.

Изменение величины, вызываемой координатой, свидетельствует о наличии соответствующего процесса.

x_k – общее обозначение координаты состояния при k-ом взаимодействии.

Примеры координат состояния системы:

Пример 1. При деформационном (механическом) взаимодействие всегда изме­няется объём W, м³. В инженерных расчетах и формулах термодинамики в основном используется удельный объем системы v,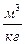

, где m – масса системы, кг.

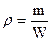- плотность.

Таким образом, X_деф – это удельный объем v.

Пример 2. Тепловое (термическое) взаимодействие:

При тепловом взаимодействии всегда имеет место обмен теплотой между системой и окружающей средой. В ходе развития науки было установлено, что координатой x_тепл является энтропия . В расчетах в основном используется удельная энтропия S

Энтропия, как параметр системы, на опыте не определяется, так как нет прибора для ее измерения. Значение энтропии вычисляются по формулам термодинамики, которые будут рассмотрены далее.

Общее определение энтропии – это мера неупорядоченности системы. Чем больше беспорядок, тем больше энтропия.

Как будет показано далее, изменение энтропии в изотермическом процессе характеризует подведенное или отведенное количество теплоты (Q_T = T∙∆S).

Таким образом, X_{тепловое(термическое)} – это S.

Пример 3. Химические реакции и фазовые превращения:

При них всегда изменяется масса компонентов системы (исходных веществ, продуктов реакции и т.д.)

m_i – масса i-го компонента системы.

Таким образом X_х-ф - это m_i.

Потенциал – это величина, разность которой у системы и окружающей среды вызывает процесс. Общее обозначение:

P_k – потенциал при k-том взаимодействии.

- потенциал окружающей среды при k-том взаимодействии;

P_kⁱ – потенциал системы при k-том взаимодействии.

Правило знаков для потенциалов:

Разность потенциалов между окружающей средой и системой считается положительной, если соответствую­щая координата при этом возрастает, и наоборот.

, если dx_k > 0

, если dx_k < 0

Найдем величины, которые являются потенциалами при наиболее распространенных взаимодействиях:

Пример 1. Деформационное взаимодействие.

Если давление над поршнем (p_н) будет больше давления под поршнем (p_вн), то удельный объем системы будет уменьшаться, то есть

при , dV<0

газ

(система)

р_вн,v

рис.1

Из этого примера следует, что давление, как потенциал, при деформационном взаимодействии не соответствует правилу знаков.

Правило знаков будет выполняться, если брать давление со знаком минус.

Таким образом,P­_деф­ – это (-p), Па

Во всех формулах термодинамики используется только абсолютное давление р.

Манометры показывают р_ман, то есть превышение давления в системе над атмосфер­ным (барометрическим) давлением В, поэтому p = p_ман +В.

Если в системе имеется разрежение (вакуум), то абсолютное давление определяется по формуле р= B – p_вак,

где p_вак – показания вакуум­метра.

Поправки для ртутных приборов:

При измерении давления ртутными приборами в мм.рт. столба следует иметь в виду, что показания этих приборов (ртутного манометра, барометра) зависят не только от величины измеряемого давления, но и от температуры ртути в приборе. При положительных температурах плотность ртути меньше, удельный объём выше, следовательно, показания приборов будут выше, чем при 0°C. При температурах ниже 0°C соотношение будет обратным. Показа­ния ртутных приборов для измерения давления всегда приводятся к 0°C.

Температуры столба ртути
Поправка на 1000 мм.рт.ст.		0,87	1,73	2,59	3,45	4,31	3,17

Для ртутного барометра, кроме таблицы поправок, также используется формула

B₀ = B(1-0.000172 t), где

где, B₀ – барометрическое давление, приведенное к 0°C;

B – показания барометра при температуре ртути t°C.

Если t>0, то поправку вычитают, если t<0 – прибавляют.

Пример 2. Тепловое взаимодействие.

Как показывает опыт, теплообмен возможен только при наличии разности температур между системой и окружающей средой. В качестве такой температуры в термодинамики используется абсолютная термодинамическая температура Т, К

T = t^°C + 273,15

t°F = t^°C + 32

Температура по шкале Фаренгейта (t°F) в термодинамике не используется.

Наиболее точно абсолютная температура определяется по показаниям газовых термомет­ров.

Пример 3. Химические и фазовые превращения.

В ходе развития науки было установлено, что потенциалом при химиче­ских и фазовых взаимодействиях является величина химиче­ского термодинамического потенциала μ_х-ф.

Большинство химических реакций и фазовых превращений протекает при одновременном постоянстве двух параметров. Например, при постоянных р и Т в термодинамике μ_х-ф обозначается как µ_р,Т и называется изобарно-изотермическим потенциалом.

Дата добавления: 2015-09-01