Читайте также:
|
Получим формулу, справедливую для любого газа (идеального, реального) и для любого процесса, включая политропный. Для простоты вывода получим формулу для массовой теплоемкости термодеформационной (тепломеханической) системы.
Из общего определения массовая теплоемкость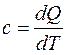 
.
Как известно из первого начала термодинамики, для термодеформационной системы
dQ = dU + pdv
Как указывалось выше, внутренняя энергия является функцией состояния, выражаемая, например формулой U=U(T,v). По правилам математики, для полного дифференциала функции нескольких переменных, в этом случае можно записать
Таким образом исходная система уравнений имеет вид:
Решая эту систему методом подстановки, получим следующее выражение
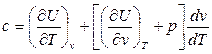(72)
Для изохорного процесса dv=0, тогда из (72)
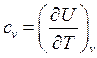(73)
Формула (73) справедлива как для идеального, так и для реального газов.
В формуле (72) необходимо знать частную производную 
для чего воспользуемся первым началом термодинамики в виде:
dU = TdS – pdv
Откуда
Частная производная в правой части
относится к 3-ему типу дифференциальных соотношений термодинамики. Тогда
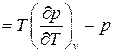(73*)
Подставим полученное выражение в формулу (72):
,
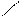
Окончательно получим
(74)
Формула (74) называется общей формулой для теплоёмкостей однородных систем и справедлива для всех процессов идеального и реального газов.
Например, массовая изобарная теплоёмкость реального газа из (74) запишется в виде
(75)
Для политропного процесса уравнение (74) приобретает следующий вид:
(76)
Дата добавления: 2015-09-01; просмотров: 126 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| II.1. Классификация теплоемкостей по единицам количества вещества и видам процессов. | | | II.3. Внутренняя энергия и теплоёмкость идеального газа. |