Примеры. f(x) = Conv{1} = {1}. Аналогично для x < 0 f(x) = Conv{-1} = {-1}

1. Пусть f(x) = |x|. Требуется вычислить f(x). Если х > 0, то f(x) = x, f ’(x) = 1, следовательно,

f(x) = Conv{1} = {1}. Аналогично для x < 0 f(x) = Conv{-1} = {-1}. Пусть х = 0. Заметим, что это единственная точка, в которой функция f(x) недифференцируема. Тогда

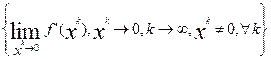= {-1, +1},

f(0) = Conv{-1, +1} = [-1, 1].

2. Пусть f(x₁, x₂) = |x₁| + |x₂|. Требуется вычислить f(x).

Заметим, что f(x₁, x₂) =

Функция f(x₁, x₂) дифференцируема в любой точке пространства, кроме точек, для которых выполнено одно из условий: |x₁| = 0 или |x₂| = 0, т.е. Q = {x R₂: x₁ = 0} {x R²: x₂ = 0}.

Пусть x 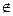Q, тогда f ’(x₁, x₂) = 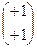, если x₁ > 0, x₂ > 0;

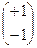f ’(x₁, x₂) = , если x₁ > 0, x₂ < 0;

f ’(x₁, x₂) = , если x₁ < 0, x₂ > 0;

f ’(x₁, x₂) = 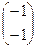, если x₁ < 0, x₂ < 0.

На Рис. 13 представлены области, в которых функция дифференцируема и значения градиентов одинаковы.

Для точек х⁰ 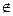Q субдифференциал состоит из единственного элемента, совпадающего с градиентом функции в этой точке.

Пусть х⁰ Q, причём х⁰ лежит на оси Ох₁ и х₁⁰ > 0. Тогда

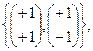= поэтому

Аналогично вычисляется субдифференциал для других точек множества Q. Таким образом,

Заметим, что некоторые свойства субдифференциалов, приведённые выше, легко получить как следствие из теоремы Кларка.

Дата добавления: 2015-09-01