Выпуклые функции

Будем рассматривать заданные на пространстве Rⁿ функции f(x), значения которых принадлежат расширенной действительной оси . Таким образом, допускается, что функции принимают значения - и + . Обозначим R₊ = R .

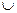
Определение. Функция f, называется выпуклой, если её надграфик epi f – выпуклое множество.

Обозначим dom f = {x: f(x)<+ }. dom f называется эффективной областью функции f.

Определение. Функцию f будем называть собственной, если f(x)> - для любых x Rⁿ и dom f 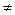0.

Пример. Функции f(x) = х² и f(x) = 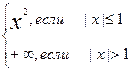являются собственными, а функция

f(x) = . не является собственной.

Теорема. Собственная функция f, является выпуклой, если и только если

f(αx + (1-α)y) αf(x) + (1-α)f(y) (1)

для любых х и у и любого α [0,1].

Замечание. Для собственных функций выполнение неравенства (1) можно рассматривать как определение выпуклых функций.

Далее мы будем рассматривать только собственные функции.

Определение. Функция f называется строго выпуклой, если

f(αx + (1 - α)y)<αf(x) + (1 - α)f(y) (2)

для любых х и у и любого α (0,1).

Определение. Функция f называется вогнутой, если функция –f является выпуклой.

Определение. Функция f называется сильно выпуклой с константой 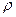>0, если

f(αx + (1 – α)y) αf(x) + (1 – α)f(y) – 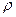α(1 – α)||x-y||² (3)

для любых х, у и любого α [0,1].

Замечание. Пусть Х – выпуклое множество, Х Rⁿ. Тогда функция называется выпуклой на множестве Х, если выполняется неравенство (1) для любых х, у Х. Аналогично определяется строго выпуклая и сильно выпуклая функция на множестве Х.

Дата добавления: 2015-09-01