выпуклого программирования градиентным методом.

Общая схема решения задач выпуклого программирования методами спуска состоит в построении последовательности

Х₀, Х₁, …, Х_k, … (8.15)

решений системы ограничений данной задачи по следующему принципу: в качестве Х₀ выбирается, вообще говоря, любая точка области решений и затем каждая последующая точка получается из предыдущей по формуле:

Х_k+1 = Х_k +λ∙ l, (8.16)

где l = (l₁, l₂, …, l_n) – некоторое направление (т.е. вектор), а λ – число, выражающее длину шага. При этом направление l и «длина шага» λ выбираются так, чтобы обеспечить сходимость последовательности (8.15) к оптимальному решению Х*. В общем случае процесс получения последовательных приближений Х_k бесконечен (и тогда некоторое Х_k0 берется за приближенное значение оптимального решения Х*), однако иногда процесс может завершиться и за конечное число шагов, приводя к локальному, а в задачах ВП и глобальному оптимуму.

Находя производную по направлению дZ/дl, мы можем определять, является ли направление l «невыгодным» или «выгодным» в смысле приближения к оптимуму.

Так как направление градиента Z целевой функции является направлением ее наискорейшего роста, то при отыскании максимума вогнутой функции (минимума выпуклой функции) в качестве l часто берется Z (- Z) и тогда формула (8.16) принимает вид

Х_k+1 = Х_k +λ∙ Z(X_k), λ>0 (если ищется Z_max) (8.17)

или Х_k+1 = Х_k -λ∙ Z(X_k), λ>0 (если ищется Z_min) (8.17′)

Методы спуска, в которых итерационная последовательность (8.15) находится по формуле (8.17) (или (8.17′)), называются градиентными.

Друг от друга они отличаются способами выбора длины шага λ и алгоритмами нахождения точки Х_k+1, если Х_k находится на границе области решений и формула (8.17) выводит Х_k+1 за пределы этой области.

Выбор длины шага λ очень важен. Как видно из рис. 8.3, перемещаясь из точки Х_о в направлении Z, мы в некоторый момент можем «проскочить» мимо точки Х₁, в которой достигается максимум.

Если величина λ выбирается так, чтобы приращение функции ∆Z при перемещении из точки Х_k в точку Х_k+1 было наибольшим (при отыскании Z_max) или наименьшим (при отыскании Z_min), то градиентный метод называется методом скорейшего спуска.

Таким образом, по методу скорейшего спуска длины шага λ в формуле (8.17) (или (8.17′)) выбирается так, чтобы при этом λ достигался экстремум функции ∆Z = Z(Х_k+1)- Z(Х_k). (Обратите внимание на то, что при нахождении точки Х_k+1 предыдущая точка Х_k считается уже известной, т.е. Z(Х_k) и ∆Z(Х_k) являются постоянными величинами, а ∆Z – функцией одной переменной λ).

Продифференцировав функцию ∆Z с учетом выражения Х_k+1 по формуле (8.17) и выражения градиента в точке Х_k, Z(Х_k)= 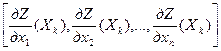, получим, что необходимое условие экстремума 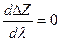примет вид:

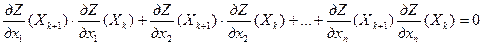(8.18)

Ему можно придать более компактную форму, если использовать скалярное произведение векторов:

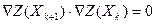(8.18′)

(Напомним, что скалярное произведение векторов в прямоугольной системе координат равно сумме произведений их соответствующих координат. Например, если l₁=(2, -1) и l₂=(3, 5), то l₁·l₂ = 2·3 +(-1) ·5 = 1. Скалярное произведение векторов равно нулю тогда и только тогда, когда они ортогональны).

Если оптимум достигается внутри области решений системы ограничений данной задачи ВП, то нет опасности, что точка Х_k+1, найденная по формуле (8.17) или (8.17′), выйдет за пределы этой области, и длину шага λ определяем по формуле (8.18) без каких-либо дополнительных ограничений.

Рис. 8.4.

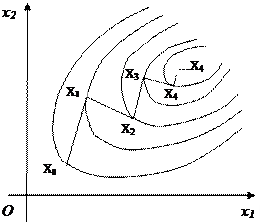Для случая двух переменных метод скорейшего спуска имеет простую геометрическую интерпретацию: для любого k луч, идущий от точки Х_k к точке X_k+1, перпендикулярен к линии уровня функции Z, проходящей через точку X_k (так как направлен по градиенту), и касается линии уровня, проходящей через точку X_k+1 (так как ввиду условия (8.17′) он перпендикулярен к следующему лучу, который в свою очередь перпендикулярен к этой линии уровня).

Таким образом, на плоскости скорейший спуск происходит по двум взаимно перпендикулярным направлениям так, как показано на рис.8.4.

Замечание. Для упрощения счета можно в формулах (8.17) и (8.17′) брать вместо Z(Хk)= с тем же направлениям, то есть координаты можно умножать или делить на положительное число.

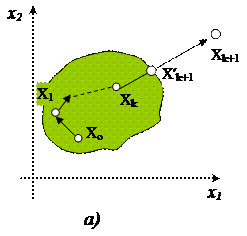
Рассмотрим теперь задачу ВП, когда оптимум целевой функции достигается на границе области решений системы ограничений. В этом случае, взяв, как и ранее, в качестве исходной точки Х₀ любую точку из области решений и находя последующие точки по формулам (8.17) и (8.17′), мы на некотором шаге получим, что X_k уже не лежит в области решений (рис. 8.5-а). Тогда вместо X_k берем точку X ′ _k, которая лежит на пересечении направления спуска с границей области решений, а все последующие точки находятся путем проектирования на эту границу точек, получаемых обычным методом скорейшего спуска.

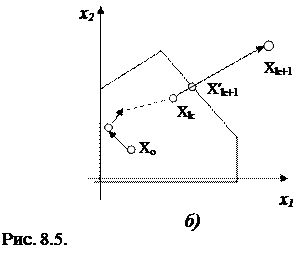Поскольку общий оператор проектирования не изучается в нашем курсе, ограничимся случаем, когда система ограничений линейная, т.е. область решений задачи для случая двух переменных ограничена отрезками прямых (рис. 8.8-б).

В этом случае система ограничений данной задачи примет вид:

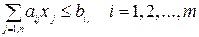(8.19)

Пусть по методу скорейшего пуска мы построили точки X₀, …, X_k, X_k+1

и убедились (подставляя в (8.19) координаты этих точек), что X₀, …, X_k лежат в области решений, а точка X_k+1 уже не лежит в ней. Значит, координаты точки X_k+1 не удовлетворяют хотя бы одному неравенству системы (8.19).

Дата добавления: 2015-09-01