
Читайте также:
|
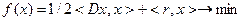 (43)
(43)
при ограничениях
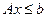 (44)
(44)
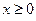 (45)
(45)
где D=|| aij || - симметрическая n x n матрица, r=(r1,…,rn) - постоянный вектор, A=|| aij || - m x n матрица, b=(b1,…,bm) - постоянный вектор, можно свести к задаче ЛП. Здесь матрица D предполагается положительно определенной (отсюда следует выпуклость квадратичной формы F(x), а ограничения (44)-(45) являются линейными). Такой переход можно осуществить следующим образом. Сначала строим каноническую форму задачи (43)-(45), введя в ограничения (44) слабые переменные xn+1,…,xn+m. Тогда ограничения задачи запишутся (в координатной форме):
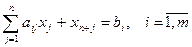 (46)
(46)
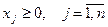 (47)
(47)
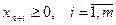 (48)
(48)
Теперь для задачи (43), (46)-(48) введем (классическую) функцию Лагранжа и запишем необходимые условия оптимальности (см. теорему 4)
- условие стационарности:
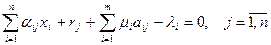 (49)
(49)
- условие допустимости;
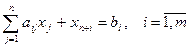 (50)
(50)
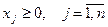 ,
, 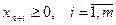 (51)
(51)
- условие дополняющей нежесткости:
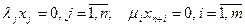 (52)
(52)
- условие неотрицательности:
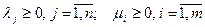 (53)
(53)
Систему (49)-(53) можно решать двухфазным симплекс-методом (методом искусственного базиса), рассматривая (49) как целевую функцию, а (50)-(53) – как ограничения, с учетом того, что множители Лагранжа l1,…, ln,m1,…, mn не должны все одновременно равняться нулю.
Замечание. При использовании двухфазного симплекс метода следует учитывать «нелинейность» ограничений (52), т.е. не включать в базисные одновременно переменные lj и xj с одним и тем же индексом и переменные mj и xn+i с одним и тем же индексом.
4) Элементарным (по своей идее) является метод сведения задачи с ограничениями-равенствами:
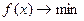 (54)
(54)
при ограничениях
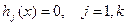 (55)
(55)
к задаче безусловной оптимизации (метод исключения). Из уравнений (55) исключается k переменных, например,
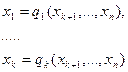
Подставляя найденные представления переменных x1,…,xk в целевую функцию (54), приходим к следующей задаче безусловной оптимизации относительно n-k переменных:
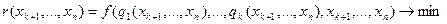
Этот метод наиболее приемлем в том случае, когда ограничения (55) линейны:
Ax=b
Дата добавления: 2015-09-04; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача дробно-линейного программирования | | | Итеративные вычислительные методы. |