Задача дробно-линейного программирования

(33)

при ограничениях

(34)

(35)

(36)

можно свести к задаче ЛП следующим образом, введем новые переменные y₀,y₁,…,y_n:

(37)

В новых переменных задача (33)-(36) запишется:

(38)

при ограничениях

(39)

(40)

(41)

(42)

где (39) и (40) получены в результате умножения обеих частей (34) и (35) на y₀ > 0; (41) получено из первого равенства (37) в результате исключения x_j; (42) аналог условия (36).

Оптимальное решение задачи ЛП (37)-(41) в Rⁿ⁺¹ найдем применяя симплекс-метод, а решение 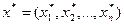исходной задачи (33)-(37) – по формуле .

Дата добавления: 2015-09-04